金属平板波导端面SSPPs反射特性研究

从第1章可知,在完美导体的表面上不支持局域性强的表面波。如果加入周期结构到光滑的金属表面,可激发SSPPs。SSPPs在一定频率范围内通过改变周期结构的几何尺寸来控制其色散特性。本节介绍在PPWG端面通过SSPPs增强反射的技术。

在前面的描述中,我们已经表征了PPWG的TE和TM的传输特性。当在平行板波导中以TEM模式传播的电磁波遇到波导终端阻抗失配时,从PPWG的特征阻抗到自由空间的阻抗(377Ω)存在阻抗的不连续性。因此,阻抗失配会导致输出端发生反射,反射率随板间距的减小而增大。

如果利用SSPPs结构构造输出端面,可以控制输出端面的特性阻抗,从而实现阻抗匹配,还可以在波导端面处实现高反射率。如图3-21所示,在PPWG上波导板和下波导板的输出端面上平行于波导的输出孔口设计周期性凹槽结构。两个波导板上的凹槽图案镜面对称。图3-21(a)为输出端面上与波导出口孔相邻的5个周期性凹槽的图案的横截面。单个槽的横截面是矩形,周期a为152μm。通过改变板间距b、凹槽深度h、结构长度d以及从第一凹槽到波导孔径边缘的距离L,可调谐SSPPs的耦合频率和强度。THz波的入射角为θ,则反射率可表征为角度的函数,如图3-21(b)所示。

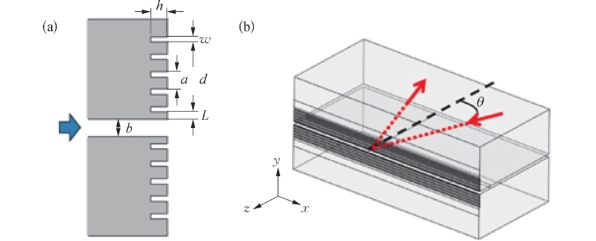
图3-21　槽形波导示意图

图3-22(a)的曲线图为入射角为0°时,反射率随频率的变化关系(参数设置如图所示)。在选定的频率(174 GHz)下,输出端面的反射率(峰值反射率)达到99%以上。红色曲线显示使用在输出端面上没有凹槽图案的PPWG的反射率。相对于没有任何凹槽图案的波导,端面做了结构化处理以后,其反射率显著增大。图3-22(b)显示了频率为174 GHz处电场分布的横截面图。大部分出射的太赫兹波能量集中在沟槽附近和波导的输出端面上,耦合到远场的能量很少。PPWG每个板上的凹槽的数量对反射率有一定影响。如图3-22(c)所示,随着凹槽数量的增加,峰值反射率增大。当凹槽数量大于4时,峰值反射率已经接近100%。

图3-22

(a)反射率与PPWG的频率的函数关系;(b)在174 GHz下,PPWG的输出端的电场分布横截面图;(c)作为每个板上凹槽数量的函数的峰值反射率

可以使用简单的RLC电路模型定性分析这种高反射率产生的物理机理(图3-23)。由于PPWG的板间距b和凹槽的尺寸在尺度上是亚波长的,所以整个结构可以表示为如图3-23(a)所示的短偶极天线。PPWG充当馈电电路,带凹槽的输出端面作为天线臂。等效电路模型如图3-23(b)所示。假设偶极天线的一个臂的有效长度x=b/2+L+ηd,其相当于相应的波导结构的物理尺寸。这里,η表示反射率接近100%时的凹槽数量。如图3-23(b)所示,当波导模式和SSPPs共振时,大部分能量集中在前3个槽中,所以η=3。在这种情况下,结构的电容近似于线性偶极子天线的电容:

根据数值模拟,当波导模式和SSPPs共振时,大部分磁场线集中在槽内,因此可以通过使用平均磁场乘以凹槽面积来估计磁通量φ。由于天线电流由PPWG馈电,不受凹槽结构的影响,因此是恒定值,所以电感大致与凹槽面积(ηah)成比例。对于图3-23(b)所示的电路,谐振频率ω=1/LC。由此,谐振频率与赝表面等离子激元结构的几何参数h、b、L和d的函数关系近似表示为(www.xing528.com)

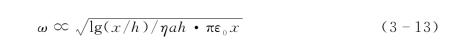
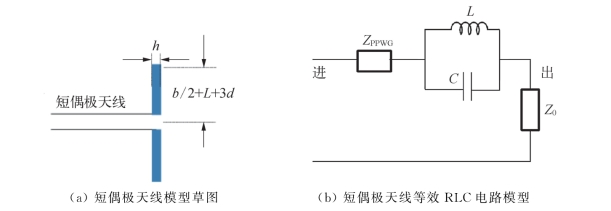
图3-23

图3-24给出了PPWG波导的传输和反射的实验结果(每个板刻蚀5个矩形槽图案)。归一化透射率定义为太赫兹波通过有凹槽和没有凹槽的相同尺寸的波导的透射谱之比。当板间距为600μm时,针对两个不同的频率197 GHz和234 GHz分别优化凹槽的参数(L,h,d和b)。图3-24(a)和图3-24(b)显示了优化后的结果。在这两种频率入射下,归一化透射率接近0%,同时归一化反射率接近于1(＞99%)。这些结果与数值模拟结果匹配。结果表明,可以通过修改金属表面结构的几何参数来调整峰值频率,同时在设计的频率下保持近乎完美的反射。值得指出的是,当输出端面没有凹槽图案时,在两个频率处反射系数均小于20%。有凹槽与没有凹槽情况下的反射率相差达到5倍。

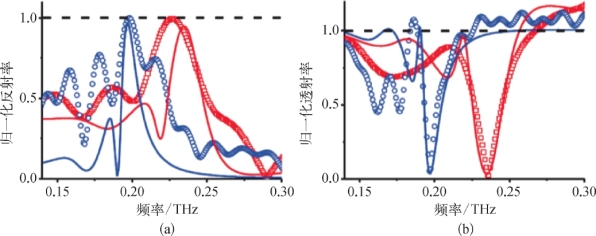
图3-24

谐振频率为197 GHz(蓝色)和234 GHz(红色)的两种不同太赫兹波导器件的归一化反射率(a)和归一化透射率(b)。圆圈表示实验结果,实线表示数值模拟的结果。波导结构参数:对于蓝色的图像,板间距b=600μm,w=152μm,L=100μm,d=475μm,h=274μm;对于红色的图像,b=200μm,w=152μm,L=228μm,d=457μm,h=205μm______________________________

利用这种端面的反射特性,我们可以设计金属平板波导的太赫兹分插复用器。以两个信道为例,上平板和下平板分别为凹槽形状、尺寸完全相同的直角梯形体分插复用器A板和分插复用器B板,两个直角梯形体板的上下两面位置上分别刻有5个凹槽,每一面的5个凹槽等距、不居中分布,两面的凹槽间距不同,无凹槽的平行面正对上下放置,中间放有等高的垫片,保证两板平行,并在板间形成一个狭缝,并使两板之间的凹槽近的一面相对,固定好后放置在水平旋转台上,如图3-25(a)(b)所示。分插复用器A板与分插复用器B板之间的距离b 1为600μm;直角梯形体的上下两面的凹槽深度h 1、h 2分别为274μm、245μm,凹槽宽度w 1、w 2分别为152μm、136μm,凹槽周期(即相邻槽之间的距离)d 1、d 2分别为475μm、425μm;第一个凹槽与最近的直角梯形体边的距离L 1、L 2分别为100μm、90μm。板间及凹槽内的介质为空气。使用时域光谱(Time-Domain Spectroscopy,TDS)系统的光电导接收器对有凹槽的两个面的输出信号进行采集,发现直角梯形体长边凹槽表面输出信号[图3-25(c)中f 1、f 1的输出面的参数为h 1、w 1、d 1、L 1]中无0.197 THz附近的太赫兹波,而直角梯形体短边凹槽表面的输出信号[图3-25(c)中f 2、f 2的输出面的参数为h 2、w 2、d 2、L 2]中无0.216 THz附近的太赫兹波。因此,当带有0.197 THz和0.216 THz的两个信道的太赫兹信号在与直角梯形体的斜面垂直的方向入射时,采集两个侧边凹槽出射的已分离的太赫兹波的信道,可实现太赫兹分插复用器的功能。

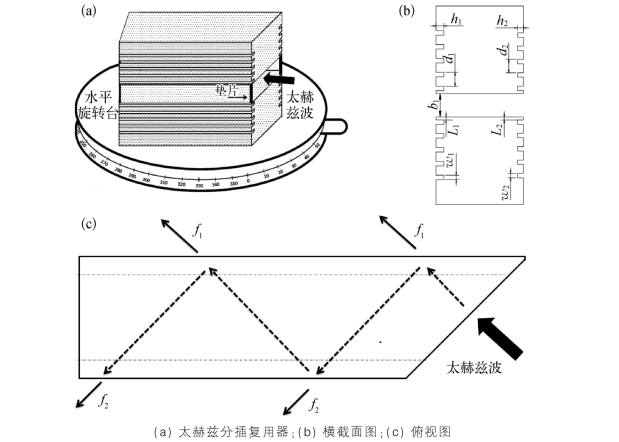
图3-25

此外,与不同介质交界处由于全反射引起的古斯-汉欣位移类似,该SSPPs耦合也会导致在反射端面中心点的位置引入一个横向偏移的量,这种横向位移Δ可类比古斯-汉欣效应。两种效应都可以解释为平行于界面的全反射效应(隐失波)产生的相位突变。在传统的古斯-汉欣效应中,隐失波的波矢量位于入射平面上,而在这里,隐失波的波矢量由垂直于入射平面的波矢分量产生。对这种古斯-汉欣位移的深入研究将有助于推动在THz频段对自旋霍尔等物理效应的理解和实现。