TE波入射与谐振特性

1.TE模的截止频率

本小节主要介绍TE波在平行板波导内的传输理论。当输入信号电场在x方向上线性偏振时(图3-8),即电场平行于波导平面时,在平行板波导中只有n阶TE n模式存在。在PPWG中的TE模的传播相当于随着入射的s偏振光在z方向上移动两个平面波在平板上来回弹跳。

图3-8　平行板波导信号传播图

此时的相位常量为

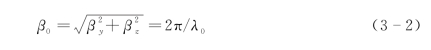
若已知平面波在金属表面的入射角θ为

则相位常数的y分量可以写为

在式(3-2)、式(3-3)中,βy和βz分别为y和z方向的相位常数;nλ0/2b≤1,所以可以得到波导在TE模式下的截止频率nλ0/2b=1,即f c=nc/2b。在式(3-3)中,λ0=c/f,可以得出入射角θ和频率f的关系图,如图3-9所示。从图中可以看出当入射波频率减小时,任何与TE n模式有关的入射角θ会变小,最终等于0°(正入射);当入射波频率增大时,角度θ变大,最终达到入射角临界值(低于90°)。对于特定的频率,角度θ越小阶数n越高。

当波导长度一定时,不仅角度会随频率的变化而变化,平面波的反射次数N也会随着频率的变化而变化,利用板间距b可以求出单位长度的平行板波导上的反射次数为

其变化规律如图3-9所示,当频率增大时,平面波的反射次数减少。

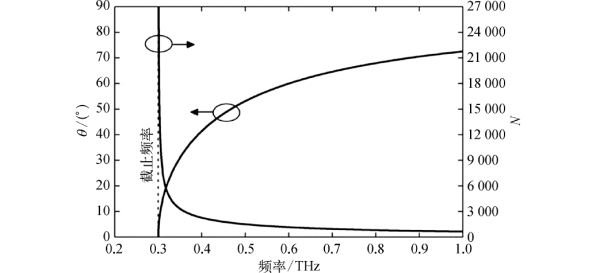
图3-9　频率与角度和反射次数的变化关系

2.TE模中的类电磁诱导透明效应及其调谐

为了研究TE波的入射以及谐振特性,我们设计了如图3-10所示的耦合器件。耦合器件形状为两个截切半圆柱(半径为32 mm),在中间制作凹槽以便平行板波导放入。金属材料使用铜。如图3-11所示,根据3.1节可知沿着L和b的方向添加两个螺旋测微器不仅可以调整位置,而且还可以减小器件的插入损耗。入射太赫兹波的偏振方向(指电场)为水平方向,以便激发低阶TE模。

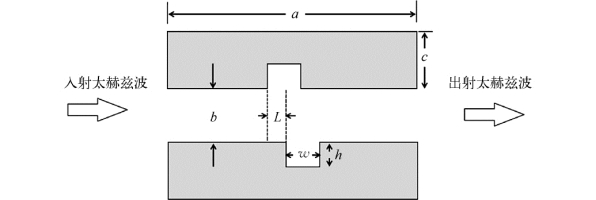
图3-10　双腔PPWG器件框图

图3-11　PPWG样品照片

首先,固定槽偏移L为200μm(槽宽w的一半),研究不同板间距b对传输特性的影响。通过对实验数据进行快速傅里叶变换(Fast Fourier Transform,FFT)后得到板间距b分别为610μm、670μm、740μm、780μm时的透射率曲线,如图3-12所示。从图中可以发现样品在0.3～0.5 THz的频段出现透射谷,透射谷的数量会随板间距d的变化而改变。当b=610μm和b=670μm时,可以观测到两个透射谷,但当b=740μm和b=780μm时,只有左透射谷存在,右透射谷退化为振荡。

然后,我们固定板间距b为650μm,改变槽偏移L,研究不同槽偏移L对传输特性的影响。使用上面类似的方法可以得到图3-13。

通过对图3-13的观察,可以发现以下两点:(1)透射谷的数量随着槽偏移L的变化而改变。在样品上下完全对称时(L=0μm),只能观测到一个透射谷,但在其他的L下,能够观测到多个透射谷。(2)随着槽偏移L的增大,左透射谷逐渐变粗,右透射谷逐渐变细。依此可以判断,在样品上下完全对称时(L=0μm),观测到的应该是右透射谷。

图3-12　不同板间距b的透射率曲线(线:模拟数据,点:实验数据)

(a)b=610μm;(b)b=670μm;(c)b=740μm;(d)b=780μm

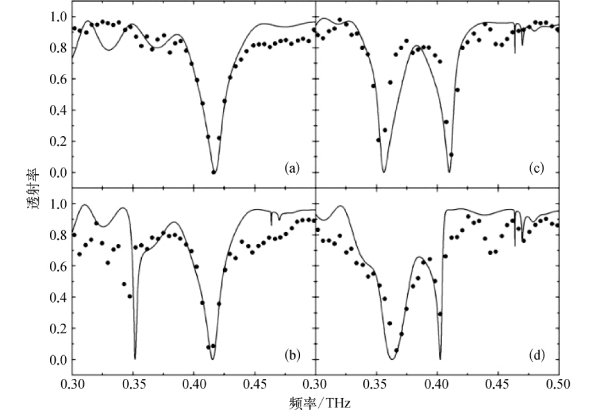
图3-13　不同槽偏移L的透射率曲线(线:模拟数据,点:实验数据)

(a)L=0μm;(b)L=100μm;(c)L=200μm;(d)L=300μm

实验中仅在某些特定值测量数据,即板间距b为610μm、670μm、740μm、780μm时和槽偏移L为0μm、100μm、200μm、300μm时的数据。若取槽偏移L=200μm,令板间距b在550～850μm变化,得到0.3～0.5 THz的透射率,如图3-14所示。

图3-14　模拟透射率与频率和板间距b的关系,此时槽偏移L=200μm

(白色虚线位置为实验中测量的板间距b)

图3-12中透射率曲线对应的板间距位置如图3-14中白色虚线所示。从图中可以清楚地看到,存在两个稳定模式(两条蓝带)。较高频的模式在b=700μm处截止,之后变为振荡,并在图3-14右上方形成爪形结构。利用这个特性可以用来制作双通道的滤波开关。

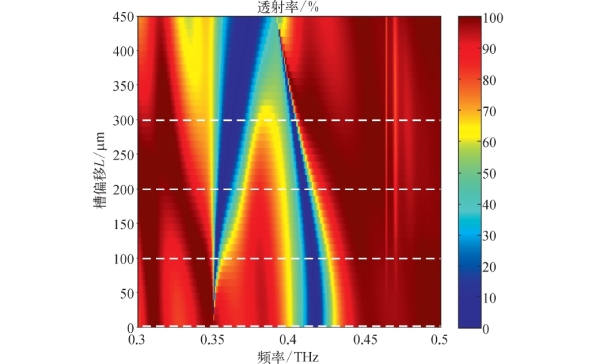
同样地,取板间距b=650μm,令槽偏移L在0～450μm变化,得到0.3～0.5 THz的透射率,如图3-15所示。从图中可以清楚地看到,同样存在两个稳定模式(两条蓝带)。较低频的模式一开始没有形成,随着槽偏移L的增大逐渐变强,对应透射谷的宽度也随之变宽。较高频的模式则呈相反的趋势,并在L=435μm处截止。对比图3-14与图3-12、图3-15与图3-13,可以发现两个数值算法的结果都与实验数据吻合得很好。

(www.xing528.com)

图3-15　模拟透射率与频率和槽偏移L的关系,此时板间距b=650μm

(白色虚线位置为实验中测量的槽偏移L)

下面讨论槽偏移和板间距影响的机制分析。我们可以发现槽偏移L产生的影响较为简单,可以归纳为上下两金属板中槽的对称性的改变,而两个凹槽相当于两个谐振腔。如图3-16所示,从模拟的电场强度分布中我们可以看出低频透射谷对应的模式应当是两个凹槽本征模式的反相耦合,高频则应当是同相耦合。反相耦合、同相耦合分别记为|ω->和|ω+>,对应透射谷的中心频率记为ω-和ω+。

图3-16　低频(a)、高频(b)透射谷中心频率的电场强度分布

当L=0时,电磁波到达两个谐振腔的时间相同,两个谐振腔本征模式几乎同时激发(相同的频率),因此只能激发电磁感生透明(Electromagnetically Induced Transparency,EIT)现象的明态。此时由于结构具有最高的对称性,反相耦合模式(反对称模式)被完全遏制,而同相耦合模式(对称模式)的强度达到最大。

当L慢慢增大时,对称性被打破。电磁波先到达上方谐振腔,后到达下方谐振腔。上方谐振腔对下方谐振腔有辐射作用,下方谐振腔在被辐射后形成暗态。反相耦合模式出现并逐渐增大,同相耦合模式则相应减少。当L达到槽宽w附近之后,下方谐振腔只能接到来自上方谐振腔的辐射,而无法通过通道内的电磁波激发。此时,同相耦合模式被完全遏制。

对于两个透射谷之间的频率,由于反相耦合模式和同相耦合模式相互竞争而抵消的作用,因此没有呈现带阻特性。而两个透射谷中心频率随槽偏移L增大而靠近,可以用一般干涉理论来解释。电磁波通过这两个谐振腔之间的光程所引起的相位差为

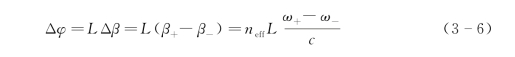
式中,c为真空中的光速;β为传播常数;n eff为有效折射率。由于是带阻特性,选取相干相消条件:Δφ=π。当L增大时,两个透射谷中心频率差减小。

板间距b产生的影响较复杂,两个透射谷的形成机理与槽偏移时基本类似,但漂移需用无槽平板的传播常数来解释。同时还伴随较高频透射谷消失的现象,需用波导理论解释。如图3-17所示,入射电磁波在波导内传输存在一定的夹角θ。如果产生谐振,必定会在竖直方向形成驻波。根据驻波波节的形成条件有

根据图3-17,入射电磁波波矢k 0的正交分解有

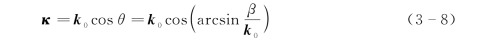
入射电磁波对应的真空中的波矢k 0仅与角频率ω有关:k 0=ω/c。

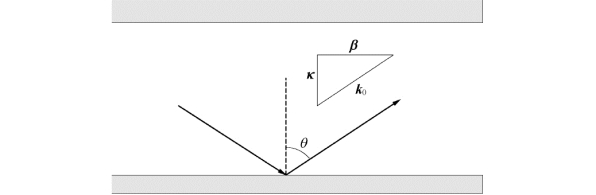
图3-17　入射电磁波波矢的正交分解

联立式(3-7)和式(3-8)得到不同频率ν和不同板间距b的传播常数β。图3-18中稳定模式中的传播常数β应当处处相等。因此图3-14中稳定模式的走向应当与图3-18中等传播常数线走向相同。

图3-18　等传播常数线图

考虑到PPWG亦是波导,所以使用能量-动量(E-p)空间描述其模式分布更为直观。做变换f=1/b,f为板间距b对应的波数(空间频率)。根据波粒二象性定律,有

式中,ћ为约化普朗克常数;h为普朗克常数。略去不影响结果的约化普朗克常数ћ,能量-动量(E-p)空间可用频率-波数(ν-f)的色散关系表示。对图3-14进行简单的变换得到图3-19。图3-14中高频透射谷的截止频率线(图中右上方的双曲线形)变换成图3-19中的直线(白色实线)。这条直线过原点,其斜率为0.3 THz/mm-1=3×108m/s,即光速线。

图3-19　样品模拟透射率T的色散关系图。虚线对应实验中测量过的板间距b,白色实线为光速线

根据已有的波导理论,在光速线上方区域(超光速区)无法激发导模,只能激发辐射模;而在光速线下方区域(亚光速区),能够激发导模,从而形成可以观测的透射谷(图3-19)。

根据式(3-7),特定入射波长λ和板间距b与能够存在的最大模式阶数n max的关系为

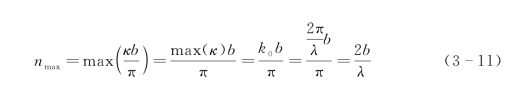
取式(3-11)中n max=1和n max=2时的极限条件并代回式(3-7),得到限制条件:b=λ/2、θ=0°和b=λ、θ=60°,其中,b=λ、θ=60°这个条件就是图3-19中的光速线,而b=λ/2、θ=0°代表了波矢只存在垂直于传播方向分量的情况。

根据b和λ的大小关系,可以将色散图分成3个观察范围(图3-19)。(1)若b＜λ/2,此时能激发的最大模式阶数n max为0,即无任何可稳定传播的模式存在。(2)若λ/2＜b＜λ,此时能激发的最大模式阶数n max为1,即仅最低阶横电模TE1得以激发。这种模式在竖直方向上满足相消相干条件:Δφ=κb=π,能够效率最大化地传输能量,为导模。(3)若b＞λ,也就是在光速线上方,此时能激发的最大模式阶数n max大于1,能够激发最低阶横电模TE1以及更高阶的横电模。高阶横电模有较多能量耗用在竖直方向上的传播,为辐射模。

图3-20为图3-19中两个特征点(A点和B点)的电场强度分布图,一张代表辐射模场分布[A点,图3-20(a)];另一张代表高频透射谷中的导模场分布[B点,图3-20(b)]。在图3-20(a)中受高阶横电模的影响,电磁波在竖直方向上未形成稳定的驻波波节。为保证水平方向形成行波,只能在竖直方向上下摆动,形成之字形路线,谐振相消引起的带阻效果较差,无法形成透射谷。而在图3-20(b)中电磁波在竖直方向上形成稳定的驻波波节,在水平方向形成行波,与两个谐振腔耦合良好,谐振相消引起的带阻效果较好,能够形成透射谷。

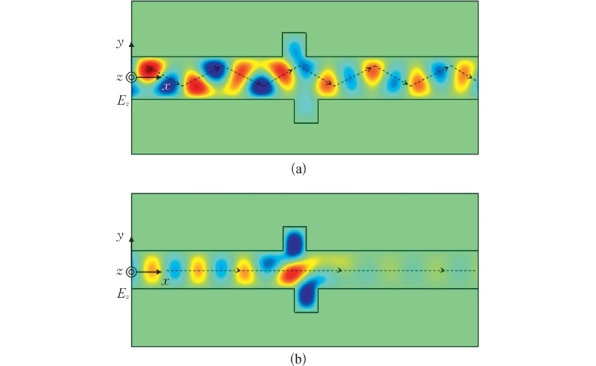
图3-20　图3-19中导模和辐射模的电场强度分布图

(a)A点:辐射模;(b)B点:导模