太赫兹表面等离激元现象及应用的THz周期金属穿孔波导

本小节介绍了利用一维周期性金属孔SSPPs实现THz波导的方法。一维周期性金属孔结构的有效介电常数与结构参数密切相关,传播的THz辐射能够很好地限制在平面表面。这种结构不仅可以实现平面THz传输,还可实现平面THz功能器件,例如Y形分束器和3 dB耦合器。

图2-16(a)为一维周期性金属孔结构的示意图,是在一个不锈钢金属板中利用传统的激光微加工技术加工一排亚波长矩形孔径。图2-16(b)所示为一维穿孔阵列的图片。穿孔阵列对TM偏振辐射具有独特的透射和色散特性,THz垂直入射样品。矩形孔的尺寸为500μm×50μm,孔的长轴平行于y轴,周期为250μm。

图2-16

(a)周期间隔矩形孔径的线性排列结构,孔槽尺寸为长s=500μm、宽a=50μm、周期d=250μm、厚l=635μm,该结构的总长度为8 mm,对应320个孔径;(b)波导的顶视图

图2-17(a)是在图2-16(a)所示的结构的一端,用化学方法蚀刻了一个半圆形的穿孔槽,将自由空间的THz辐射耦合到THz波SSPPs上。半圆形穿孔槽的半径为1 cm,宽为300μm,深为100μm,圆心与第一个金属孔径重合。实验时使用电光晶体来测量波导上不同点的电磁辐射特性。图2-17(b)为有限差分时域(Finite-Difference Time-Domain,FDTD)法仿真的传输透射的归一化结果[t WG(ω)]。图2-17(c)～(e)为每个谐振模式的凹槽中y-z平面的总电场分布。从图2-17(b)～(e)可以看出,低频振荡对应SSPPs模式,能量局限在槽与金属交界处的表面,如图2-17(c)所示;高频共振为介质波导模式,能量在槽的上表面和下表面来回振荡并产生驻波,如图2-17(d)(e)所示。

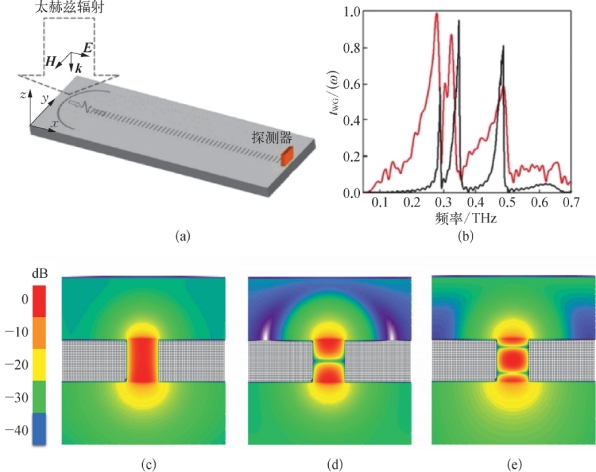
图2-17

(a)实验示意图,半圆形槽用于将单周期THz脉冲耦合和聚焦到平面SSPPs结构上,利用ZnTe晶体进行电光采样检测导波;(b)THz的透射谱,红色曲线为实验结果,黑色曲线为FDTD仿真结果;(c)～(e)矩形孔径中y-z平面的总电场分布,分别对应TM100、TM101和TM102的谐振模式(www.xing528.com)

图2-18(a)为沿波导的长度(x轴)方向测量的电场分量E z的大小,可以得出波导损耗为0.013 mm-1。图2-18(b)表示在y轴两个不同传播位置(5 cm和7 cm)处截面的电场分布的大小。在两个横截面上的电场分布呈高斯型,半峰全宽(Full Width at Half Maximum,FWHM)为2.2 mm,表明在沿波导传播的SSPPs模式的横向方向上电场的约束能力强。图2-18(c)为电场分量E z在波导表面上沿z轴的大小,观察到电场会以指数形式从金属介质界面上衰减。1/e的衰减长度是1.69 mm,是平板金属表面的。从图2-18中可以明显看出,SSPPs模式在穿孔的金属波导上显示出紧密的约束和低的传播损耗。

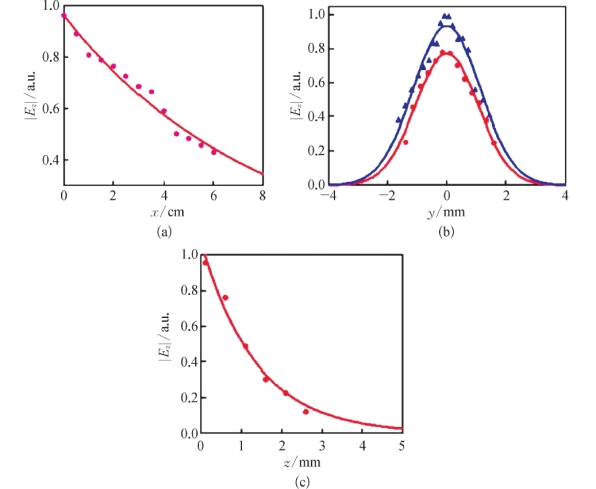
图2-18　平面SSPPs波导中TM100模式的传播特性

(a)电场振幅|E Z|沿x轴的大小变化;(b)在y轴的两个不同传播位置(5 cm和7 cm)测量的电场振幅|E Z|;(c)在样品表面沿z轴测量的电场振幅|E Z|

基于等离子波导的强束缚性特点,可以实现简单的功能器件,例如Y形分束器和3 dB耦合器。图2-19(a)(b)为利用SSPPs结构制作的这两种波导器件的导波特性。图2-19(a)为Y形分束器的结构示意图,它由一个32 mm长的输入波导、两个32 mm长的斜臂(旋转11.2°)和两个32 mm长的输出部分组成。Y形分束器的总长度为95.4 mm,两臂之间的中心到中心的间距为11.6 mm。自由空间THz辐射通过蚀刻的半环形槽与波导装置耦合。将实验测量的E z的数据用两个空间错开的高斯函数拟合(实心红线)。两个高斯函数的中心位置在y=-5.8 mm和y=5.8 mm处,与Y形分束器的两个输出臂的中心重合。两个高斯函数的半峰全宽分别为2.31 mm和2.34 mm,与图2-19(a)中Y形分束器的功能一致。图2-19(b)为3 dB耦合器的结构示意图。中间耦合区域的中心距为1.55 mm,长度为3 cm,3 dB耦合器的总尺寸为169 mm×12.2 mm。图2-19中的点为测量的电场分量E z在y方向上的大小。拟合的两个高斯函数的中心位置出现在波导中心,半峰全宽分别为2.12 mm和2.27 mm,实现了3 dB耦合器的耦合功能。

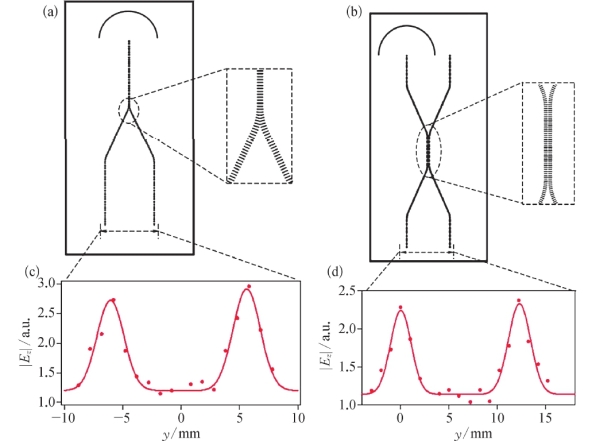
图2-19　Y形分束器和3 dB耦合器示意图

(a)Y形分束器的结构示意图;(b)3 dB耦合器的结构示意图;(c)(d)分别为在Y形分束器和3 dB耦合器的末端沿y轴测量的电场振幅|E Z|,点为实验结果,线为拟合结果(红线是利用两个空间偏移高斯函数的和来拟合实验数据的)