太赫兹表面等离激元及色散方程应用

SPPs正是由金属的特殊光学性质决定的。它是在介电常数完全相反的两种材料的交界面上(在光波段通常指金属-介质交界面),自由电子与入射场相互作用产生的一种电磁模式,如图1-1所示。可从最基本的麦克斯韦(Maxwell)方程组入手,对它的物理机制进行了解,并对SPPs的色散关系进行公式推导。

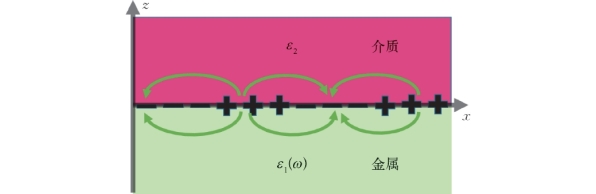
图1-1　半无限大的金属-介质交界面表面等离激元的产生

考虑到两个半无限大的交界面(图1-1),上半部分空间(z＞0)是介电常数为ε2的电介质,下半部分空间(z＜0)是介电常数为ε1(ω)的金属。交界面上形成的SPPs电磁波,沿x方向传播,在垂直于界面的z方向上呈指数衰减。

假设电磁波的电场是TM极化(p波,即电场E在x和z方向上均有分量,磁场H只有在垂直于纸面的y方向上有分量)的情况,上半区(z＞0)的电场和磁场可表示为

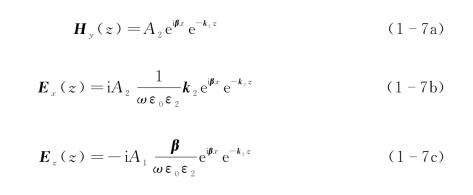
下半区(z＜0)的电场和磁场可表示为

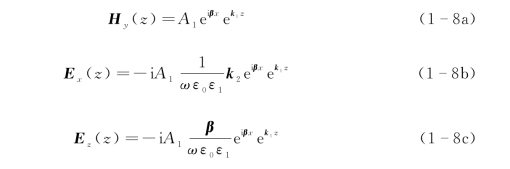
式中,k 1、k 2是沿z方向的波矢量,它的倒数决定了电磁波在z方向上的衰减长度,可用来表征电磁波的束缚程度;β是电磁波沿交界面(x方向)的波矢量。

根据电磁波的连续性边界条件,在交界面处(z=0)的E x(z)和H y(z)连续:

由于表面波在垂直交界面的方向上是指数衰减,则必须满足k 1＞0、k 2＞0的条件,因此要使式(1-9b)成立,则需要满足ε2和ε1的符号相反,例如光频段内的金属与介质。将上面的H y代入波动方程

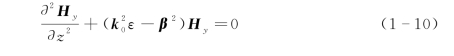(https://www.xing528.com)

可得

最后可以得到半无限大的金属-介质交界面上SPPs的色散关系:

类似地,对于电磁波的电场是TE极化(s波,即磁场H在x和z方向上均有分量,电场E只有在垂直于纸面的y方向上有分量)的情况,上半区(z＞0)的

电场和磁场可表示为

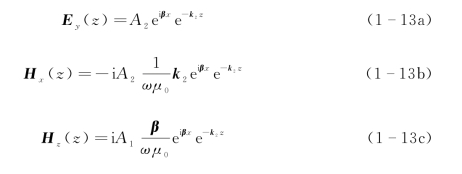
下半区(z＜0)的电场和磁场可表示为

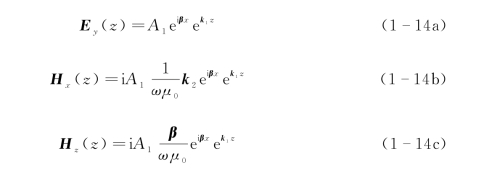
同样根据电磁波的连续性边界条件,在交界面处(z=0)的切向电场和磁场连续,即H x(z)和E y(z)连续,由此可得

由于SPPs是表面波,所以式(1-15a)中的k 1和k 2必须同时满足大于0,则此式中A 1=0,也就是A 1=A 2=0。然而这样的电磁波并不存在,从数学的角度证明了SPPs只能是一种TM极化的电磁波。