太赫兹表面等离激元：金属性质和介电常数

SPPs是指在金属表面存在的自由振动的电子与光子相互作用产生的沿着金属表面传播的电子疏密波。众所周知,在低频的条件下,金属中的电磁场以迅衰场的形式存在,可以认为金属是理想的导体。在可见光和近红外区域,其复介电常数的实部相对于虚部是一个非常大的负数。正因为金属具有这样的光学属性,使得金属和介质的界面处可以传输SPPs,另外夹于两介质中间的金属薄膜可以被用来传输长程SPPs。

金属的良导体属性,与它极高的电导率有关,一般而言,材料的光学性质可以由介电常数这个物理量完整描述。金属作为一种色散材料,其介电常数与入射光的频率紧密关联,表现出明显的色散性质。因此,针对金属材料,我们需要建立合适的色散模型对其光学性质进行描述。

由于金属中存在大量可以自由移动的电子,我们通过利用基于自由电子气体的模型[德鲁德(Drude)模型]来推导金属介电常数的表达式。Drude模型是1902年由P.Drude提出的。这个模型描绘的物理图像是金属中的自由电子与其他电子或者原子核之间的电磁场间不存在任何相互作用,金属的物理性质完全由自由电子运动和外加电磁场相互作用决定。当受到外加电磁场作用时,电子在牛顿运动定律的制约下运动。另外,电子的运动将会受到晶体中的原子核、杂质或晶格缺陷产生弹性碰撞等的影响而被散射至其他方向。假设电子质量为m,电荷为-e,在外电场E中运动,则电子的运动方程表示为以下形式:

式中,γ是电子振动的阻尼系数,也称为碰撞频率,用来描述电子之间碰撞的概率,一般取值为1013～1014s-1,折合到频率为1.6×1012～1.6×1013Hz;τ=1/γ,为自由电子的弛豫时间。

假设外场是时谐场,即E=E 0e-iωτ,上述运动方程解的形式为x=x 0e-iωτ,代入式(1-1)不难得到(https://www.xing528.com)

所有自由电子在外场作用下的诱导偶极矩P=n·(-ex)表示为

根据D=ε0E+P,可以求得电位移矢量为

式中,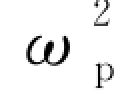=(ne 2)/(mε0)为自由电子气体的等离子体频率。因此,我们可以得到金属介电常数的表达式:

值得注意的是,这种简单的Drude模型在低频下能够很好地与实验数据值吻合。在高频段(如紫外波段),ω≫ωp,由于存在能带间电子跃迁,Drude模型误差极大。此时,考虑到带间跃迁的影响,需要引入Lorentz-Drude模型进行修正,并引入无穷大频率处的介电常数ε∞。