曲线积分和曲面积分计算实现

一、曲线积分

函数f（x，y）在曲线弧L上的第一类曲线积分定义为

其中，Δs1，Δs2，…，Δsn为曲线弧被任意分割成的n个小弧段的弧长；λ＝为第i个小弧段上任意取定的一点（i＝1，2，…，n）.

设f（x，y）在曲线弧L上有定义且连续，L的参数方程为

x＝φ(t)，y＝ψ(t)，(α≤t≤β)

其中，φ（t）、ψ（t）在[α，β]上具有一阶连续导数，且φ′2（t）＋ψ′2（t）≠0，则

上述公式可以推广到空间曲线Γ由参数方程

x＝φ(t)，y＝ψ(t)，z＝ω(t)，(α≤t≤β)

给出的情形，这时有

根据上述求曲线积分公式，可以利用MATLAB提供的求导函数diff和求定积分函数int来求解第一类曲线积分.

例5.16　计算曲线积分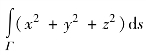，其中Γ是螺旋线：x＝acos t，y＝asin t，z＝kt，在0≤t≤2π之间的一段弧.

解：

函数P（x，y）在有向曲线弧L上的对坐标x的曲线积分定义为

其中，M1（x1，y1），M2（x2，y2），…，Mn-1（xn-1，yn-1）是将L分割成n个有向小弧段的任意点列；Δxi＝xi-xi-1；Δyi＝yi-yi-1；λ为各小弧段长度的最大值；（ξi，ηi）为第i个有向小弧段上任意取定的一点（i＝1，2，…，n）.

类似地，函数Q（x，y）在有向曲线弧L上的对坐标y的曲线积分定义为

以上两个积分也称为第二类曲线积分，应用上经常将两者合并起来写成

设P（x，y）、Q（x，y）在有向曲线弧L上有定义且连续，L的参数方程为

x＝φ(t)，y＝ψ(t)

当参数t由α单调地变到β时，点M（x，y）从L的起点沿着L运动到终点，φ（t）、ψ（t）在α和β为端点的闭区间上具有一阶连续导数，且φ′2（t）＋ψ′2（t）≠0，则

上述公式可以推广到空间有向曲线Γ由参数方程

x＝φ(t)，y＝ψ(t)，z＝ω(t)

给出的情形，这时有

因此，仍然可以利用diff函数和int函数来求解第二类曲线积分.

例5.17　计算曲线积分，其中Γ是从点A（3，2，1）到点B（0，0，0）的直线段AB.

解：Γ的参数方程为

x＝3t，y＝2t，z＝t，t从1到0(www.xing528.com)

因此，编写如下语句求解该曲线积分：

二、曲面积分

函数f（x，y，z）在曲面Σ上的第一类曲面积分定义为

其中，ΔS1，ΔS2，…，ΔSn为曲面Σ被任意分割成的n个小块曲面（ΔSi同时也代表第i小块曲面的面积）；为第i个小块曲面上任意取定的一点（i＝1，2，…，n）.

设f（x，y，z）在Σ上连续，Σ的方程为

z＝z(x，y)，(x，y)∈Dxy

且z（x，y）在Dxy上具有连续偏导数，则

由上面给出的求曲面积分公式，可以利用MATLAB提供的求偏导函数diff和求积分函数int来求解第一类曲面积分.

例5.18　计算曲面积分，其中Σ是球面x2＋y2＋z2＝4被平面z＝1所截出的顶部.

解：Σ的方程为

变换到极坐标系下通过解二重积分来求解上述曲面积分，编写如下语句：

函数R（x，y，z）在有向曲面Σ上对坐标x、y的曲面积分定义为

其中，ΔS1，ΔS2，…，ΔSn为曲面Σ被任意分割成的n个有向小块曲面（ΔSi同时也代表第i小块曲面的面积）；为ΔSi在xOy面上的投影；（ξi，ηi，ζi）为第i个小块曲面上任意取定的一点（i＝1，2，…，n）.

类似地，函数P（x，y，z）和Q（x，y，z）在有向曲面Σ上对坐标y、z和z、x的曲面积分分别定义为

以上三个曲面积分也称为第二类曲面积分，应用上经常将三者合并起来写成

设R（x，y，z）在Σ上连续，Σ的方程为

z＝z(x，y)，(x，y)∈Dxy

且z（x，y）在Dxy上具有连续偏导数，则

其中，曲面积分取Σ上侧时等号右端取正号，取Σ下侧时等号右端取负号.

类似地，有

根据上述公式，可以嵌套调用int函数来求解第二类曲面积分.

例5.19　计算曲面积分，其中Σ是球面x2＋y2＋z2＝1外侧在x≥0，y≥0的部分.

解：将Σ分为Σ1和Σ2两部分，其中

因此

编写如下语句求解该曲面积分：