二次规划是非线性规划中一种特殊情形，它的目标函数是二次实函数，约束是线性的.由于二次规划问题比较简单，易于求解，某些非线性规划也可以转化为求解一系列二次规划问题，因此，二次规划算法较早引起人们的重视，成为求解非线性规划的一个重要途径。
二次规划的标准形式为
MATLAB中对应的标准形式：
MATLAB调用格式：
x＝quadprog（H，f）：无约束条件；
[x，fval]＝quadprog（H，f，A，b，Aeq，beq）：约束中含有线性不等式约束或等式约束；
[x，fval]＝quadprog（H，f，A，b，Aeq，beq，lb，ub）：变量有下界和上界；
[x，fval，exitflag，output，lambda]＝quadprog（H，f，A，b，Aeq，beq，lb，ub，x0，options）：x0为迭代初值，返回exitflag参数，描述计算的退出条件.返回包含优化信息的结构输出output，返回解x处包含拉格朗日乘子的lambda结构参数.其中options表示优化参数，可选择3种算法之一：trust-region-reflective、interior-point-convex、active-setactive-set.options缺省时，默认算法trust-region-reflective，其他算法可通过optimset或optimoptions完成，如：
例4.25 求解下面的最优化问题：
解：首先，目标函数可以写成下面的矩阵形式
输入下列系数矩阵：
然后调用二次规划函数quadprog：
得问题的解：
第4章练习题
1.已知向量u＝[2，1，5，2]T和矩阵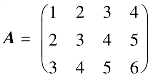
，求：
（1）Au；（2）uTAT；（3）AT；（4）提取第2条对角线元素；（5）提取第2条对角线以上的元素.
2.生成以下矩阵：
（1）3×3零矩阵；（2）3×6全1矩阵；
（3）与矩阵A同型的标准形矩阵，其中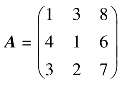
.
3.已知方阵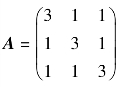
，求：
（1）A＋2E；（2）A的每个元素加2；（3）A的行列式；（4）A的逆；（5）把A旋转90°；（6）特征值及一组特征向量；（7）A的迹.
4.求下列矩阵的行列式、逆、特征值和特征向量.
5.将向量组α1＝[1，1，1]，α2＝[1，2，2]，α3＝[1，1，3]正交规范化.
6.求一个正交变换x＝Py，把二次型
f＝2x1x2＋2x1x3-2x1x4-2x2x3＋2x2x4＋2x3x4(www.xing528.com)
化为标准形，写出此标准形.
7.设多项式f（x）＝5x4-2x3＋2x2-2，g（x）＝2x-1，计算它们的乘积及除法，求f（x）的所有根.
8.用二次多项式拟合下列数据：
拟合结果画图比较.
9.选择一些函数，在n（如5～11）个结点上用分段线性和三次样条插值方法，计算m（如50～100）个插值点的函数值.通过数值和图形的输出，将两种插值结果与精确值进行比较.适当增加n，再作比较，由此做初步分析.下列函数供选择参考：
(1)y＝sin x，0≤x≤2π；
(2)y＝(1-x2)1/2，-1≤x≤1；
(3)y＝cos10x，-2≤x≤2；
(4)y＝e-x2，-2≤x≤2.
10.画图并求函数y＝x sin（x2-x-1）在（-2，-0.1）内的零点.
11.解线性方程组.
（1）
，求唯一解；
（2）
，求通解.
12.求解线性规划问题：
min z＝-x1-2x2＋x3-x4-4x5＋2x6
s.t. x1＋x2＋x3＋x4＋x5＋x6≤6
2x1＋x2-2x3＋x4≤4
x3＋x4＋2x5＋x6≤4
xj≥0，(j＝1，2，…，6)
13.求使函数f（x）＝-5x1-4x2-6x3取最小值的x值，且满足约束条件：
14.求解Rosenbrock函数
的极小值，初始点选为x0＝（-1.2，2）.
15.设有400万元资金，要求4年内使用完，若在一年内使用资金x万元，则可得效益
万元（效益不能再使用），当年不用的资金可存入银行，年利率为10%.试制订资金的使用计划，以使4年效益之和为最大.
16.解非线性规划问题
17.求解二次规划
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
