MATLAB软件实验：矩阵范数与条件数

一、向量的3种常用范数及其计算函数

设向量V＝（v1，v2，…，vn）.

（1）2-范数

（2）1-范数

（3）-范数

在MATLAB中，求这3种向量范数的函数分别为：

①norm（V）或norm（V，2）：计算向量V的2-范数；

②norm（V，1）：计算向量V的1-范数；

③norm（V，inf）：计算向量V的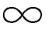-范数.

例如：

二、矩阵的范数及其计算函数

设A是一个m×n的矩阵，V是一个含有n个元素的列向量，定义：

‖A‖＝max‖A⋅V‖，‖V‖＝1.

因为A是一个m×n的矩阵，而V是一个n维列向量，所以A⋅V是一个m维列向量.对应前面定义的3种不同的向量范数，定义3种矩阵范数，这样定义的矩阵范数‖A‖称为矩阵从属于向量的范数.

上式只给出了矩阵范数的基本定义，未给出具体计算方法，完全按照上式是难以计算一个矩阵的某种具体范数的.设矩阵A＝（aij）m×n，则从属3种向量范数的矩阵范数计算公式是：(www.xing528.com)

，其中λ1为最大特征值（为A的共轭转置）

MATLAB提供了求3种矩阵范数的函数，其函数调用格式与求向量的范数的函数完全相同，这里不再赘述.例如：

三、矩阵的条件数

在求解线性方程组AX＝b时，一般认为，系数矩阵A中个别元素的微小扰动不会引起解向量的很大变化.这样的假设在工程应用中非常重要，因为一般系数矩阵的数据是由实验数据获得的，并非精确值，但与精确值误差不大，上面的假设可以得出如下结论：当参与运算的系数与实际精确值误差很小时，所获得的解与问题的精确解误差也很小.遗憾的是，上述假设并非总是正确的.对于有的系数矩阵，个别元素的微小扰动会引起解的很大变化，在计算数学中，称这种矩阵是病态矩阵，否则为良性矩阵，条件数就是用来描述矩阵的这种性能的一个参数.

矩阵A的条件数等于A的范数与A的逆矩阵的范数的乘积，即

cond(A)＝‖A‖⋅‖A-1‖

这样定义的条件数总是大于1的.条件数越接近于1，矩阵的性能越好；反之，矩阵的性能越差.按照前面定义的A的3种范数，相应地可定义3种条件数.在MATLAB中，计算A的3种条件数的函数是：

①cond（A，1）：计算A的1-范数下的条件数，即

cond(A，1)＝‖A‖1⋅‖A-1‖1

②cond（A）或cond（A，2）：计算A的2-范数下的条件数，即

cond(A)＝‖A‖2⋅‖A-1‖2

③cond（A，inf）：计算A的范数下的条件数，即

例如，对上面A：

一个矩阵和它的逆矩阵一定具有相同的条件数.另外，对于秩为0或非常接近0的奇异矩阵，其条件数会非常大，也即矩阵病态程度很严重.