计算机基本运算方法揭秘

计算机中的CPU能直接提供的运算有算术运算和逻辑运算，其运算的过程有两个行为：一个是运算结果；另一个是运算状态。比如加减法运算是否产生了进位或借位，计算结果是否产生了溢出，计算的结果是不是零等，这些状态往往是发出控制命令的依据，所以我们更应该掌握这些状态的变化。80x86把这些状态存放在一个状态标志寄存器FLAG中。

图1.9所示的是一个16位的寄存器，其中空白位表示没有使用或者其他与运算无关的状态，除空白位外的位表示运算状态。CF表示进位或借位，当进行加减法运算有进借位时，CF=1，否则CF=0。SF标志位表示运算的结果是不是负数，如果运算结果最高位是1，代表是负数，则SF=1，反之SF=0。ZF是0标志，如果计算的结果是0，则ZF=1，反之ZF=0。AF是辅助进位标志，PF是奇偶标志，OF是溢出标志。

图1.9　16位寄存器

1）补码运算及溢出的判断

（1）补码运算

计算机中有符号数一般用补码来表示，补码的加减法运算规则如下：

若进行X+Y运算，则利用CPU内部的加法器可直接计算得到：[X]补+[Y]补=[X+Y]补。

若进行X-Y运算，则需将其转换为X+（-Y），此时只需将-Y转换为补码，仍可通过加法器来实现：[X]补-[Y]补=[X-Y]补=[X]补+[-Y]补。

例：求-97的原码、反码和补码（8位表示）。

解：97=64+32+1　二进制为：1100001

原码为：11100001B

反码为：10011110B

补码为：10011111B

例：已知（X）补=11101110B，求其原码和十进制真值。

解：X为一负数，原码为数值部分求反加1。

（X）原=10010010B

真值X=-18D

例：用补码表示形式计算11-7=？

解：11-7=4=11+（-7）

（11）补=0　0001011　（-7）补=1　1111001

（11）补-（7）补=（11）补+（-7）补=1 0 0000100

取低八位　=00000100　（多出来的第9位1自动丢弃）

对应真值=4

结果正确。

（2）溢出的判断

计算机中的有符号一般用补码来表示，补码的表示范围和位数有关，如果超界了就会得到一个错误的结果。就像一个钟表，它的表示范围是0～12点，如果8点再过5小时，应该是8+5=13，然而由于钟表的表示范围有限，结果在表盘上看到是1点。很显然8+5=1这个结果是错误的，这就是溢出，这是因为13超出了钟表的表示范围。

相对于其他状态的判断，溢出的判断较为复杂，对运算结果是否有溢出的判断，可通过“双进位”法来进行。

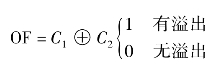
其中C2是数据最高位向符号位的进位，如果有进位C2=1，否则C2=0；C1其实就是CF。

例：设字长为8位，用补码进行计算（+120）+（+30）

结果代表-106，结果错误，C1=0，C2=1，OF=C1⊕C2=1(www.xing528.com)

例：设字长为8位，计算-5-16=（-5）+（-16）

结果代表-21，结果正确，

从上面的运算可以看出，符号位也参与了运算。

2）逻辑运算

逻辑运算是按照二进制的最小单位Bit（位）来进行的，常用的逻辑运算有：与运算、或运算、异或运算、非运算等。

（1）与运算

与0相与得0，与1相与保持不变，利用与运算可以将指定位清零。

例：10110110∧11110000

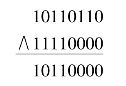
上例中高四位都和1进行与，低四位都和0进行与，结果就实现对原数的低四位清零。

（2）或运算

与1相或得1，与0相或保持不变，利用或运算可以将指定位置1。

例：00000110∨00110000

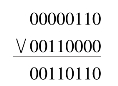
上例中通过或运算把数字06H变成了36H，通过对照ASCII表可以发现36H正好是数字6的ASCII，这个例子实现了数字6转化为6的ASCII，即6→‘6’。

另外ASCII表中大写A的ASCII是41H，小写字母a的ASCII是61H，二者只有第5位不同，通过修改第五位就可改变大小写。例：

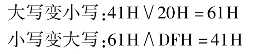
“A”～“Z”的ASCII码41H～5AH；“a”～“z”的ASCII码61H～7AH；“0”～“9”的ASCII码30H～39H。从上面的例子可以看出使用合适的与、或运算，能够实现大小写的转换，也能够实现数值和ASCII的转换。

（3）异或运算

与1相异或等于取反，与0相异或保持不变，利用异或运算可以对指定位求反。

例：00000110⊕00000100

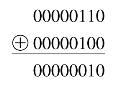
计算机控制的点动开关就是通过异或运算来实现的，按一次开，再按一次关。每按一次开关都和1进行异或运算即可。

（4）非运算

按位取反，利用非运算可以对所有位求反。

3）BCD码运算及十进制调整

由于计算机总是将数据作为二进制数来进行运算，在利用指令进行算术运算时，是按“逢16进一”的法则进行，而日常生活中采用的十进制运算均是按“逢10进一”的法则进行，故两种计算方法中相差6。因此，需要进行“十进制调整”。

十进制调整的规则如下：

若BCD码加法运算结果中出现无效码或出现进位，则在相应位置再加6。若BCD码减法运算结果中出现无效码或出现借位，则在相应位置再减6。

实际上，分离BCD码的十进制调整处理方法略有不同，在高4位上还需加F。