1)十进制、二进制和十六进制之间的关系
计算机中的数字用高低电平表示,高电平代表1,低电平代表0,或者相反。也就是说,计算机只能操作二进制数,而人们日常只习惯使用十进制,人要和计算机打交道就要进行进制之间的转换。先把十进制转换为二进制,交给计算机进行运算,计算机运算的结果再转换成十进制输出给用户,整个流程:十进制→计算机系统(二进制处理)→十进制。于是,就有了二-十进制的转换,二-十进制之间的转换,“数字电路”和“计算机文化基础”课程已经讲述过这些,此处不再赘述。
十六进制其实是二进制的简化写法,每四位二进制数对应一位十六进制数,比如二进制数10100101,十六进制则写为A5,很显然用二进制表示需要写8位,而十六进制则只需写2位。
十六进制→二进制,例如:
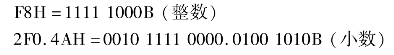
二进制→十六进制,例如:
1001111001010.010111B如何转换为十六进制呢?具体操作是以“.”为准,以四位二进制数为一组,向左右分段,不足四位添0凑够四位。过程如下:
![]()
二进制数在末尾标注B,十进制数在末尾标注D(也可省略),十六进制数在末尾标注H(C语言编程一般在首部标注0x,例如0x2A)。
2)机器数和真值
计算机只认识0和1,所以无论是数值还是符号都用0和1来表示。通常专门用一个数的最高位作为符号位:0用来表示正数,1用来表示负数。以八位二进制数为例,比如:
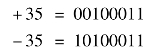
这种在计算机中使用的、连同符号位一起数字化了的数,就称为机器数。机器数所表示的真实值则称为真值。如机器数10100011所表示的真值为-35(十进制)或-0100011(二进制),可以看出在机器数中,用0、1取代了真值的正、负号。
机器数可以有不同的表示方法,对于有符号数,机器数常用的表示方法有原码、反码、补码、移码4种;对于浮点数又引入了移码表示。
(1)原码
按照机器数的表示方法,即最高位表示符号、数值位用二进制的绝对值表示的方法,便称为原码表示法。设机器数位长为n(通常值为8,16,32等),则数X的原码可定义为:
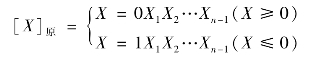
n位原码表示的数值范围是:
![]()
对应于原码的111…1~011…1。
数0的原码有两种不同的表示形式:
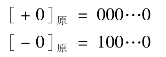
原码表示简单、直观,与真值之间的转换方便,但是使用原码做加减法运算不方便,比如:
![]()
很显然这个结果是不正确的,还需要对运算进行处理,因此操作起来不方便。另外,数0有+0和-0两种表示方法,也就是说0的表示不唯一。
(2)反码
正数的反码和原码相同;负数的反码是将其对应正数各位(连同符号位一起)取反得到,或者将原码除符号位外其余各位取反,反码的定义可表示为:
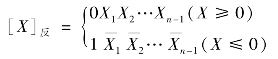
n位原码表示的数值范围是:
![]()
对应于反码的100~0~011…1。
同样,数0的反码也有两种不同的表示形式:
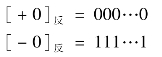
使用反码做加减法运算可以纠正原码计算的一些错误,比如:
![]()
但是反码与真值之间的转换不直观,反码还原为真值的方法是:反码→原码→真值。数0还是有+0和-0两种表示方法。
(3)补码
正数的补码和原码相同;负数的补码是将其对应正数各位(连同符号位一起)取反再加1,或者将原码除符号位外其余各位取反再加1,补码的定义可表示为:
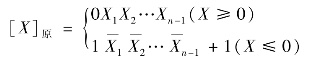
n位补码表示的数值范围是:(https://www.xing528.com)
![]()
对应于补码的100…0~011…1。
数0的补码只有一种表示形式:
![]()
使用补码做加算术运算,在数值表示范围内可以得到正确合理的结果,比如:
![]()
正是因为补码具有这两个明显的优势,所以计算机中的有符号数一般都使用补码来表示和运算。
(4)移码
移码(又称增码)是符号位取反的补码,它和原码、反码和补码不同,它不会用来直接表示一个数,而是用来表示浮点数的阶码。也就是说,它是用来表示浮点数的一部分,而不是直接用来表示一个完整的数。定点数表示数的范围受字长限制,表示数的范围有限,定点表示的精度有限。机器中常用定点数表示纯整数和纯小数。
例如,IEEE754标准浮点数表示:
对任意一个二进制数N,总可以写成:
![]()
式中,E为数N的阶码,M为数N的尾数,S用来表示符号位。
阶码用移码、尾数用原码,尾数的最高位恒为1(如上式1.M),该1在尾数中不表示出来。
①单精度格式:32位,符号位1位,阶码8位,尾数23位,如图1.7所示。

图1.7 单精度格式
②双精度格式:64位,符号位1位,阶码11位,尾数52位,如图1.8所示。

图1.8 双精度格式
例:用32位单精度表示-108.0125。
解:-108.0125D=(-1)∗1101100.000000110011001100…B
=(-1)∗26∗1.101100 000000110011001100…B
S=1B E=6+127=133=10000101B 阶数范围-127~128
M=101100 00000011001100110B(如果超过23位则弃掉后面的数位)
表示结果:1 10000101 101100 00000011001100110(32位)
十六进制表示为:0xC2D80666,即0xC2D80666代表十进制-108.012 5
以8位二进制数为例,我们可以比较各种表示方法之间的区别,见表1.1。
表1.1 有符号的表示方式
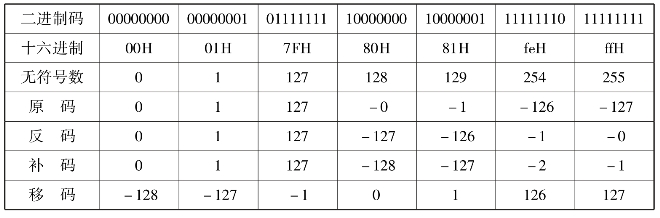
3)编码
计算机中除了数字还有符号,比如“abc”这些字母,只用来显示输出和输入,对它们进行运算是没有意义的,这些符号也是以二进制存储在计算机中的,最常见的就是ASCII码;还有一种常用的编码BCD码,称为二进制编码的十进制数,是为方便进行特定计算而制定的编码规则。
用4位二进制数表示1位十进制数的编码方法称为BCD码,之所以称为二进制编码的十进制数,是因为BCD码只使用了十六进制的前0~9这10个符号,去除了a~f这6个符号。这样BCD还是二进制数,看起来却像是十进制数一样。但是必须要清楚BCD码毕竟是二进制编码,只是看起来像是十进制。比如:
![]()
如果去掉了27H后面的“H”,那么看起来就是十进制27,这就实现了二进制看起来和十进制一样(如果不看后面的H),但是它并不是十进制。同时因为去掉了a~f,所以BCD码也不是二进制,它的正确叫法是二进制编码的十进制数。
计算机里的BCD码表示方法又分为两种:组合BCD码和分离BCD码,见表1.2。
表1.2 BCD码

如果是组合BCD码,一个字节单元可以存放两个BCD码;如果是分离BCD码,一个字节单元只能存放一个BCD码。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




