对于LDA 边缘类问题，文献[121]提出了有效的应对之策。具体做法是：在计算满足式（4-23）的情况下，对一些比较接近的类的距离而言，边缘类和其他比较接近的类相隔的距离要大得多，以至于边缘类主导了特征分解，致使降维投影矩阵太过强调一些已经分开的、较好的类别，由此引发了邻近类重叠的问题。对此，文献[121]用式（4-24）重新定义Sb来解决这个问题。
有人提出对Fisher 准则实施加权的方法，如文献[122]用式（4-25）对Fisher 准则做了重新定义。
有人提出通过核函数来优化LDA 方法[123]。主要思想如下：充分利用各种矩阵使样本空间发生变换，即从之前的空间Rn转变成现在的F 空间，旨在充分利用非线性变换方式将空间Rn的非线性图形变成线性图形，使之变得更加简单，从而使传统的LDA 法应用起来更加方便。
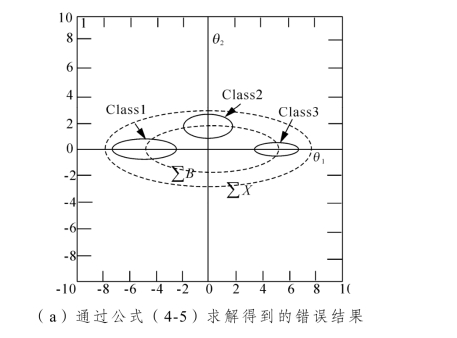
文献[124-126]指出了LDA 法存在的第三个问题：当Sb的某一特征向量与St或Sw的其中一个特征矢量斜率相同或相近时，由式（4-5）所得到的结果无法确保贝叶斯误差是最小的，具体参照图示4-2。
(www.xing528.com)
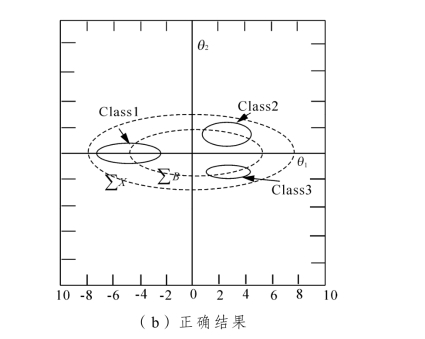
图4-2
这两个图示包含了三类，分别代表一个高斯分布，其中，∑B =Sb，∑X =St，Sb, St的首个特征向量是一致的，即：e1= w1= u1。通过式（4-5）将特征空间降到一维情况下，对于图4-2（a），若选用e2投影结果，类1与类3 的重叠会非常严重，而图4-2（b）的结果正确。据此可见，该式求解的投影结果无法确保分类的准确性。
文献[124-126]提出了有效的应对之策：对样本所属类进行重新分类，让其形成子类，继而使矩阵Sb发生变化，这就是子类判别分析方法（SDA）。使用子类旨在减少此类向量的斜率相同或相近的状况。用表示最后类别的个数，可通过式（4-26）来求解。
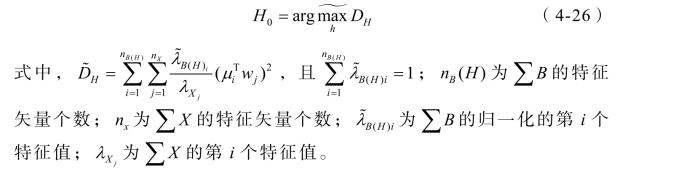
使用LDA 优化的人脸识别方法种类众多，大多数都是围绕小样本、过度强调边缘类这两个问题加以优化的[127-130]，此处不再逐一介绍。而对于文献[124-126]涉及的问题，在LDA 运用于人脸识别过程中一般并不多见，可忽略不计。本书围绕这两个问题给出了一种经过改进的LDA算法，下面将重点阐述。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
