PCA+LDA方法在人脸检测与识别研究中的应用

主分量分析法作为使用全局统计特征及无监督的一种识别法，对于模式识别而言，在特征选取方面是非常有效的。它基于最小方差准则，利用投影把高维空间中的数据映射在一组正交集之上，并按照从大到小的顺序将得到的值排序。只要所选的方差贡献率充足，用此方法就可把前M 个特征向量组建而成的空间当作低维投影空间，再充分运用投影空间来降低数据的空间维数，即由之前的R 维下降至M 维，即M≪R ，继而实现数据降维的效果，且完好地将数据里面的主要信息保存下来。其具体流程为：按照列把所有的人脸图像变成M×N 维列向量，图像的大小是M×N，可将其当作M 维空间中的一个点，具体参照图4-1。

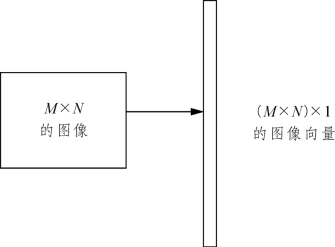
图4-1　PCA 算法中将图像表示为列向量

设训练样本数为K，其编号为 A1, A2, …, AK，那么，可用 x1, x2,…, xK来代表图像的列向量，可利用公式（4-6）来求解K 个样本图像的均值向量。

向量的协方差矩阵用式（4-7）来计算。

围绕C 展开特征分析，求解相应的特征向量μi，且满足|| μi||= 1；在计算过程中，对称矩阵C 的大小是(M ×N)2，即便是尺寸不大的图像，其维数也是非常之大。可见，若对其特征值与向量直接计算，计算量是非常大的，因此，使用线性代数理论来求解XXT的特征值λi及其相应的特征向量μi，并对其进行转化，使之变成求解

的特征值 λi和向量 vi。这里，XTX 的维数只有N × N，比 XXT的维数(M ×N)2小得多，运算量明显降低。通过式（4-8）可对矩阵 L 进行对角化。

式中，V =[V1, V2,… , VK]；λi为L 的特征值；vi为与之相应的特征向量；{v1,v2,…,vk}为标准坐标系； Λ 为对角矩阵。

对角线上的元素为L 矩阵的特征值，成功求解vi之后，就可以用式（4-9）来求解ui。(www.xing528.com)

通过上述公式求得的结果为所求图像的特征向量，这是对较低维矩阵 L 的特征值与向量进行求解间接得到的。根据大小顺序，对应特征值与特征向量分别为： λ1≥ λ2≥ …≥ λK, u1, u2, …, uK。

因此，可对所有的人脸图像进行投影，将之投影到子空间中，这个子空间是通过 u1, u2, …, uK构建而成的。本章给出的经过优化的 LDA 算法也是使用这种方式使运算量降下来的。

对比M×N，K 更小一些，不过，一般而言，K 还是非常大。事实上，并不是全部的μi均具有非常大的保留意义，出于压缩运算量的考虑，可利用式（4-10）计算出前p 个特征向量。

式（4-10）中， Φ( p)是一个整数，比1 小，它代表的是前p 个样本集的能量在总体能量中所占的百分比，其取值通常为0.9。

Belhumeur 将PCA 法的特征与LDA 的缺点有机融合起来进行考虑，提出了PCA+LDA 方法。此法充分运用主分量分析对高维空间的样本进行投影，以降低空间维数，由此确保类内离散度矩阵Sw非奇异。首先，采用PCA 法将值代入式（4-11）计算出最优投影矩阵Wpca。

其中，Wpca为与St的p 个最大特征值相应的特征向量。其次，再对全部样本进行投影，将之投影至这个空间中，并在这个空间中展开计算，求得类间与类内两个散度矩阵。利用公式（4-4）和式（4-5）计算出投影矩阵的秩，再通过式（4-12）求解投影空间。

该法[115]使类内离散度矩阵Sw奇异这一难题迎刃而解，不过，先通过公式（4-12）进行降维处理会造成类内离散度矩阵零空间的丢失。鉴于此，学者们着手探讨其他有效解决LDA 问题的途径。