基于多元统计模型的分形小波自适应图像去噪方法

本章提出一种基于多元统计模型的分形小波自适应图像去噪算法[92]。根据分形小波变换具有低熵性、多分辨率、去相关性和选基灵活性等特点，通过选用扩展的 GGD 模型中的 MGGD（multivariate generalized gaussian distribution）模型[93]，在建立多元统计模型基础上利用分形小波变换来完成图像去噪。即通过最小化残差1R 得到最接近 p1( x→) 的p2( x→)以及自适应调整参数α 和β ；通过使用四叉树分割来实现对噪声图像自适应地预测分形小波无噪图像编码，达到去噪的目的。与其他算法相比较，这种算法具有更好的去噪效果和更强的边缘保持能力，而且特别适用于消除高斯和脉冲混合噪声。

2.1.2.1　多元统计模型的贝叶斯估计

设 IA为不带噪声的自然图像， IB为带噪声图像，它们之间的关系可以用式（2-14）来表示：

其中，C 表示零均值高斯白噪声， C ～ N(0,1)；σ 2表示噪声方差。

对噪声图像 IB进行多分辨率分形小波分解后得到第j 层第i 个水平小波系数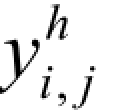、垂直小波系数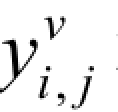和对角小波系数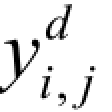。由小波变换的线性关系，可以得出：

在计算过程中，关注的焦点是未知小波系数向量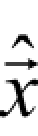的估计值，而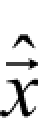的估计值的计算又依赖于噪声图像 IB所对应的小波系数向量y→。本章利用最大后验概率（maximum a posteriori，MAP）算子最大化概率 p (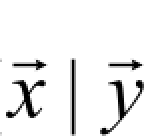)来估计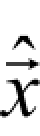，可以通过式（2-17）来计算。

其次，必须为 p (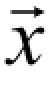→)建立合适的统计模型。为此，对样本图像的小波系数进行检测，发现它们的分布近似于高斯分布，再结合文献[94-96]，得出高斯混合模型最适合组建最佳模型。因此，选用扩展的GGD 模型中的MGGD 模型可表示为：

其中，α 和β 为模型的球形参数；ν 是α ,β 和协方差矩阵∑x→的归一化常数。如果把式（2-17）中的ln p (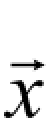)定义为未知函数 f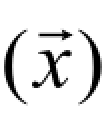，则由式（2-17）和式（2-18）可得：

最后，利用式（2-21）对式（2-20）进行化简可得：

这样，假设μ =0 ，利用MGGD 模型可以得出式（2-22）的更明确的计算式：

由式（2-22）和式（2-23）可得：(www.xing528.com)

为了解决式（2-24）中没有通解的问题，可以通过定义α ,β 及协方差矩阵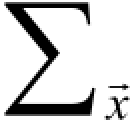为特殊值或数值来达到求解的目的。本章在实验中采用最小二乘法自适应求解参数α 和β 。

2.1.2.2　算法描述

利用基于多元统计模型的分形小波自适应图像去噪算法进行去噪的具体步骤描述如下：

Step 1：对含噪图像进行同态变换。通过同态变换，含乘性噪声的原图像 IB转换为只含加性噪声的图像 IB′。

Step 2：先对含噪信号 f ( k) 进行分形小波变换，选择合适的小波基和小波分解层数j，得到相应的小波系数。

Step 3：选择MGGD 多元统计模型自适应求解参数α 和β 。在对自然图像的小波系数分布情况进行分析后，通过下面的方法来获得最适合的参数值α 和β 。

众所周知，自然图像的小波系数的详细分布看起来像零均值高斯分布，如GGD，所以选用20 幅大小为512×512 的测试图像进行样本系数提取。在分析过程中，利用Daubechies 20 滤波器对图像集进行分形小波分解，以寻找最接近每个子带分析的MGGD 多元统计模型，此时，确定最适合的参数问题就可以转化为数据拟合问题。如果考虑两个分布函数均方差，残差的 2L 范数可以用式（2-25）来定义：

由于没有样本时， p1(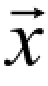→) 可能为0，以及当 p1(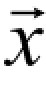→) 取值小得不合理时，利用lsqcurvefit（）函数可能得到不准确的解，这时，通过观测获得风险值2R 以及参数α ,β 之间的关系。

Step 4：对分解得到的小波系数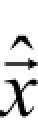和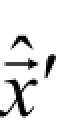，利用2.1.1.5 部分中介绍的分形小波编码方法对噪声图像进行无噪预测编码。

Step 5：利用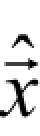和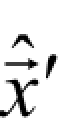进行小波重构，得到估计信号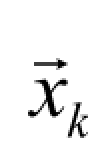和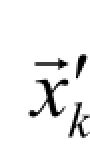，即去噪后的图像信号。