常用强度理论及ANSYS14.0实例解析

由于材料破坏的基本形式可分为脆性断裂和塑性流动两类，相应的强度理论也可以分为关于脆性断裂破坏的强度理论和关于塑性流动破坏的强度理论两类。前者如最大拉应力理论、最大拉应变理论；后者如最大切应力理论和形状改变比能理论。

1．最大拉应力理论

最大拉应力理论又称为第一强度理论。十七世纪时，T程上使用的材料主要是砖、石、铸铁等，材料的破坏形式主要是脆性断裂，因此出现了最大正应力理论，后来修正为最大拉应力理论。这个理论认为，使材料发生断裂破坏的主要因素是最大拉应力，即不论材料在什么复杂应力状态下，只要最大拉应力达到由简单拉伸试验所测得的极限应力σ_lim，就会引起材料的断裂破坏，其破坏条件为σ=σ_lim，将极限应力除以安全系数n，得到许用应力［σ］。于是，据此理论建立的强度条件为

σ1≤［σ］ (21-32)

试验表明，对于砖石、铸铁等脆性材料，此理论较为适合，如铸铁等脆性材料在甲．向拉伸时，断裂破坏发生在拉应力最大的横截面卜^，扭转破坏也发生在拉应力最大的斜截面卜。但是，此理论没有考虑其他两个主应力σ₂和σ₃对材料破坏的影响，而且对于没有拉应力的应力状态（如单向压缩、三向压缩等）也无法应用。

2．最大拉应变理论

最大拉应变理论又称为第二强度理论．这一理论是由最大线应变理论修正得到的。这个理论认为，使材料发生断裂破坏的主要因素是最大拉应变，亦即不论材料在什么复杂应力状态下，只要最大拉应变达到了简单拉伸发生破坏时的极限值ε_jx时，就会引起材料的断裂破坏，因此破坏条件为ε₁=ε_jx。假设材料在断裂破坏前，始终服从虎克定律，即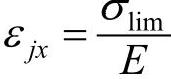，则把广义虎克定律代入后，可得出以主应力表示的破坏条件σ₁−μ（σ₂+σ₃）=σ_lim，将σ_lim除以安全系数，得到许用应力，于是据此理论建立的强度条件为

σ₁−μ（σ₂+σ₃）≤[σ] （21-3）

这个理论可以较好地解释岩石等脆性材料在单向压缩时沿纵向开裂的脆断现象，但并不为金属材料的试验所证实。根据对塑性材料的强度研究，它和某些实验相矛盾，另外在各方向均匀压缩时，这个理论也未被证实。实验表明，该理论只适用于脆性材料。

3.最大切应力理论

最大切应力理论又称为第三强度理论，十九世纪开始，工程上大量使用钢材，这些材料塑性性能好，其主要破坏形式是塑性流动。这个理论认为，使材料发生流动破坏的主要因素是最大切应力，亦即不论材料在什么复杂应力状态下，只要最大切应力达到了简单拉伸时的极限值τ_s，就会引起材料的流动破坏。这一极限值就是材料在单向拉伸出现流动时的最大切应力。因此破坏条件为

τ_max=τ_s

在三向应力状态下

在单向拉伸下出现流动时的最大切应力τ_s与极限应力σ_s的关系为

于是，流动破坏条件可表示为(www.xing528.com)

σ₁−σ₃=σ_s

将σ_s除以安全系数得到许用应力[σ]，于是据此理论建立的强度条件为

σ₁−σ₃≤[σ] （21-4）

这个理论也称为屈雷斯卡（H.Tresca）理论。一些试验结果表明，最大切应力理论对于塑性材料是相当符合的，在机械工程中得到了广泛应用。但是这个理论忽略的中间主应力σ₂的影响，使得在二向应力状态下计算结果偏于安全。

4.形状改变比能理论

形状改变比能理论又称为第四强度理论。它认为形状改变比能是引起材料流动破坏的主要因素。亦即不论材料在什么复杂应力状态下，当形状改变比能达到某一极限值时，材料就发生流动破坏，这个极限值就是材料在单向拉伸下发生流动时的形状改变比能u_jx。

三向应力状态下的形状改变比能，即

在计算单向拉伸下出现流动时的形状改变比能时，令上式中的σ₁=σ_s，σ₂=σ₃=0，即可得

对应于这个理论的流动破坏条件为

将σ_s除以安全系数得到许用应力[σ]，于是据此理论建立的强度条件为

或

这个理论也称为米赛斯（R·Von·Mises）理论，对于钢材等塑性材料，这个理论与实验结果很符合，在二向应力状态下，比第三强度理论更接近实际，是目前对塑性材料广泛采用的理论。

以上列举的四个强度理论，在工程设计中得到了广泛的应用。应该指出，由于材料的破坏形式不仅与材料本身的性质有关，而且与材料所处的应力状态有关。即使同一种材料在不同的应力状态下也可能有不同的破坏形式。因此，严格地说，应根据材料的破坏形式而不是根据材料来选择相应的强度理论。但一般说来，脆性材料在通常的情况下，以脆性断裂的形式破坏，所以宜采用第一和第二强度理论，而塑性材料在通常的情况下却大多产生塑性流动形式的破坏，所以宜采用第三和第四强度理论。但是，无论是塑性材料或脆性材料，在三向拉应力接近相等的情况下，都以脆性断裂形式破坏，所以应采用第一强度理论，而在三向压应力接近相等的情况下，都可引起塑性变形，所以应采用第三或第四强度理论。