ANSYS14.0工程实例：动力学基本方程解析

1.瞬态动力学方程

ANSYS计算动力学的基本方程是

式中，{u}为节点位移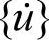；为节点速度，{u}为节点加速度，[M]为总体质量矩阵；[C]为总体阻尼矩阵；[K]为总体刚度矩阵；{F}为结构的外载荷。ANSYS提供了两种总体质量矩阵：一致质量矩阵（默认）和集中质量矩阵。设置方法：勾选面板中的Use lumped mass approx。

总体质量矩阵由密度参数生成，因此进行动力学分析时必须输入密度。式（21-9）为瞬态动力学的基本方程，ANSYS使用三种方法求解式（21-9），分别是完全法，模态叠加法和缩减法。完全法和缩减法采用直接积分求解瞬态动力学平衡方程，即使用Newmark方法和改进后的HHT方法；模态叠加法使用坐标转换把式（21-9）进行解耦后开始求解。

2.模态方程

将式（21-9）中的[C]和{F}取0，则转换为模态分析的基本方程

ANSYS假设模态分析为线性行为，因此总体质量矩阵和总体刚度矩阵都为常量。 对于线性系统，式（21-10）解的形式为

式中，{φ}_i为第i阶模态对应的振型特征向量；ω_i为第i阶模态的固有频率（单位：rad/s）；t为时间（单位：s）。

将式（21-11）代入式（21-10）中，整理后得

式（21-12）的另外一种表述为(www.xing528.com)

[K]{φ_i}=ω²_i[M]{φ_i} （21-13）

ANSYS提供了5种方法，求解式（21-12）。在下一小节中将详细介绍。

3.谐响应方程

在谐响应分析中，结构中的所有节点都以相同频率，不同的相位运动。结构中各点的阻尼不同，导致相位的不同。结构的位移表达式如下

式中，u_max为最大位移；i为单位复数，即-1的方均根；Ω为强迫圆频率（rad/s）=2 πf；f为强迫频率（Hz）；t为时间；Φ为位移相位偏移（单位：rad）。

力矢量指定为与位移具有相同表达式，即

式中，F_max为力幅值；Ψ为力的相位

将式（21-14）和式（21-15）代入式（21-9）中，得

式（21-16）就是谐响应求解的基本方程。ANSYS提供了完全法、缩减法和模态叠加法三种求解方法，来求解式（21-16）。