【摘要】:在线性或非线性瞬态分析中,使用子步满足瞬态时间累积法则。在谐响应分析中,使用子步获得谐波频率范围内多个频率处的解。平衡迭代是在给定子步下为了收敛而计算的附加解,对于非线性求解的收敛起着重要作用。图21-12 三个载荷步的载荷-时间曲线图21-13 载荷步、子步和平衡迭代第一个载荷步,将载荷逐渐加到5~10个子步以上,每个子步仅用一次平衡迭代。第二个载荷步,得到最终收敛解,且仅有一个使用15~25次平衡迭代的子步。
载荷步是为了成功求解模型的一种必要设置。在线性静态分析中,可以使用不同的载荷步施加不同的载荷组合如在第一个载荷步中施加风载荷,在第二个载荷步中施加重力载荷,在第三个载荷步中施加风和重力载荷以及一个不同的支承条件等等。在瞬态分析中,多个载荷步加到载荷-时间曲线的不同区段。
ANSYS程序将把在第一个载荷步选择的单元组用于随后的所有载荷步,而不论用户为随后的载荷步指定哪个单元组。要选择一个单元组,可使用下列两种方法之一。
命令:ESEL
GUI:Utility Menu→Select→Entities
图21-12为三个载荷步的载荷-时间曲线:第一个载荷步是线性斜坡载荷,第二个载荷步是恒定载荷,第三个载荷步是突然卸载载荷。
子步是执行求解载荷步中的点。使用子步,有如下原因。
(1)在非线性静态或稳态分析中,使用子步逐渐施加载荷以便能获得精确解。
(2)在线性或非线性瞬态分析中,使用子步满足瞬态时间累积法则。
(3)在谐响应分析中,使用子步获得谐波频率范围内多个频率处的解。(https://www.xing528.com)
平衡迭代是在给定子步下为了收敛而计算的附加解,对于非线性求解的收敛起着重要作用。
例如,在二维材料非线性分析中,为获得精确解,通常使用两个载荷步(图21-13)。
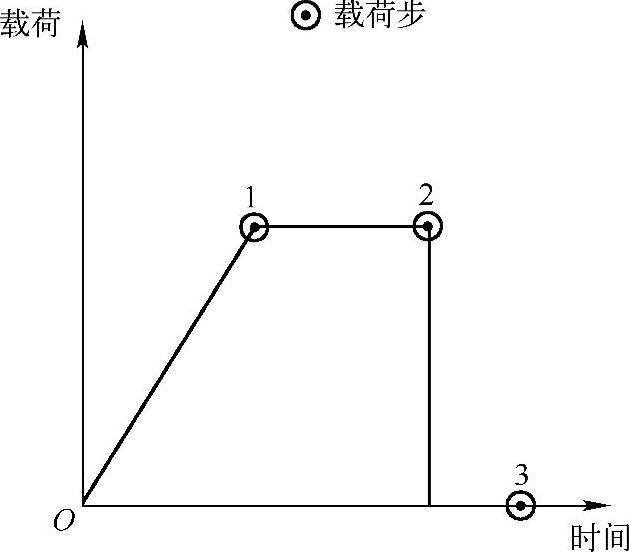
图21-12 三个载荷步的载荷-时间曲线
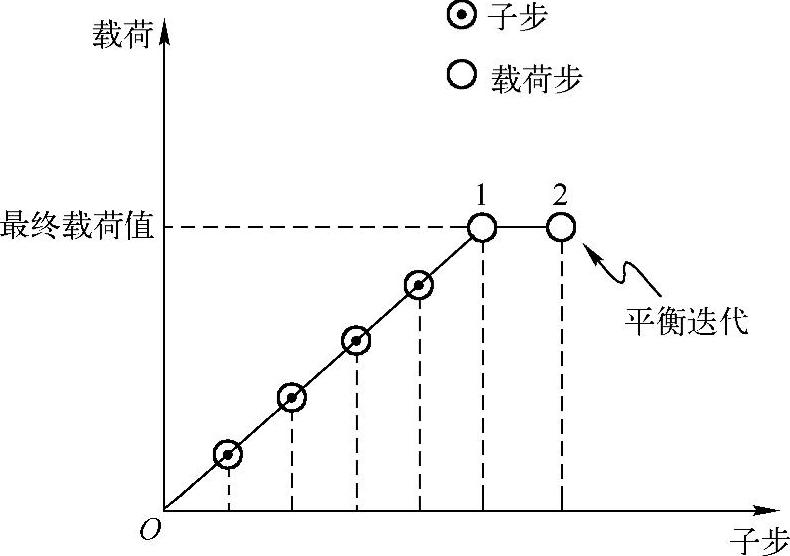
图21-13 载荷步、子步和平衡迭代
第一个载荷步,将载荷逐渐加到5~10个子步以上,每个子步仅用一次平衡迭代。 第二个载荷步,得到最终收敛解,且仅有一个使用15~25次平衡迭代的子步。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




