典型约束方程应用案例

1.约束方程的定义

线性约束方程提供了一种比简单耦合更通用的联系自由度值的方法。约束方程必须有如下形式：

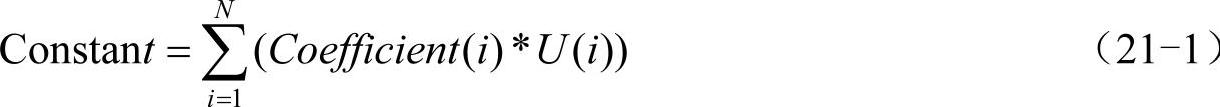
式中，U（i）是自由度项（i），N是方程中项的编号。

2.定义约束方程

（1）直接方法

可用下列方法直接生成约束方程。

命令：CE

GUI：单击Main Menu→Preprocessor→Coupling/Ceqn→Constraint Eqn，弹出定义约束方程的面板，如图21-10所示。

该面板包括11个控制选项，分别是约束方程参考号（NEQN），方程常数（CONST），约束方程表达式中第一项中的节点号（NODE1），约束方程表达式中第一项中的约束自由度（Lab1），约束方程表达式中第一项中的常数（C1），约束方程表达式中第二项中的节点号（NODE2），约束方程表达式中第二项中的约束自由度（Lab2），约束方程表达式中第二项中的常数（C2），约束方程表达式中第三项中的节点号（NODE3），约束方程表达式中第三项中的约束自由度（Lab3），约束方程表达式中第三项中的常数（C3）。

图21-11是一个典型的约束方程应用的例子，力矩的传递是由梁单元与平面单元的连接来完成的。(www.xing528.com)

在此例中，如果不用约束方程则节点2表现为一个铰链。可用下列方法传递梁和平面应力单元之间的力矩：

ROTZ2=（UY3−UY1）/10

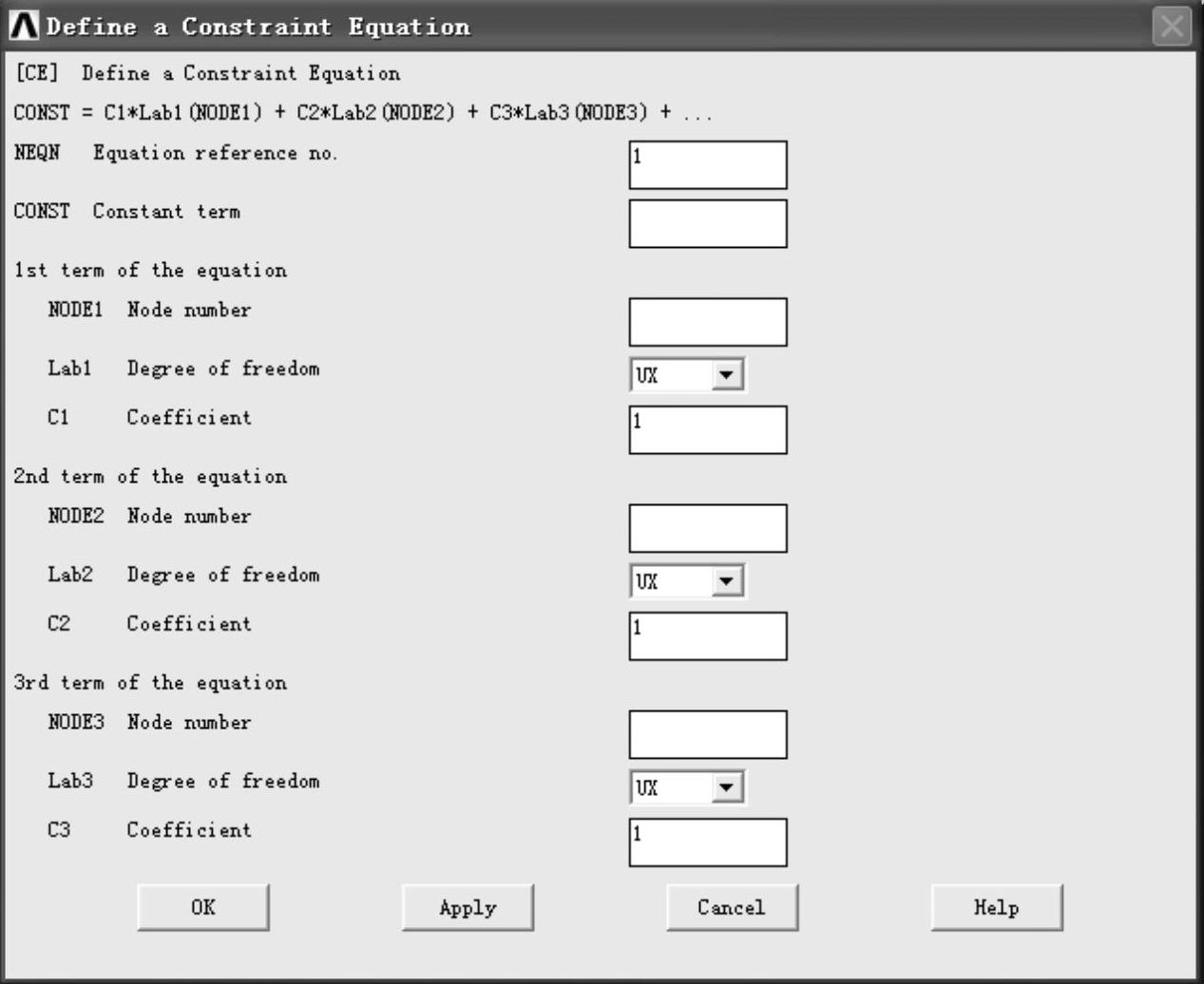
图21-10 定义约束方程的面板

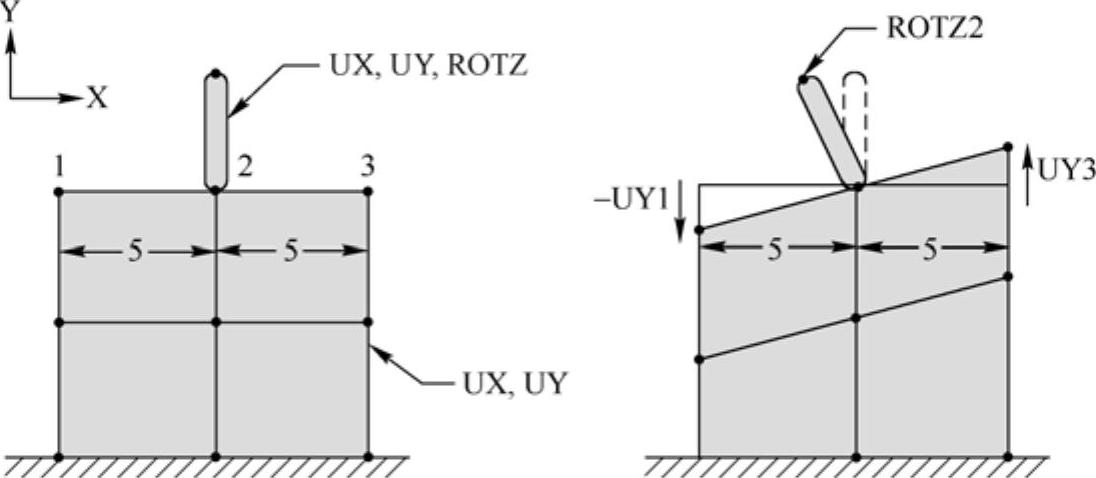
图21-11 建立旋转和平移自由度的关系

此方程应当重写成要求的格式，并代入程序：

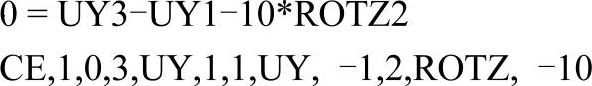
方程中第一个独特的自由度按方程中所有其他自由度的方式删除。一个独特的自由度是不在任何其他约束方程、耦合节点集、给定位移集或主自由度集中定义的自由度。应将方程的第一项作为自由度删除。尽管在理论上可在多于一个方程中指定相同的自由度，但用户必须小心避免重定义，还必须保证模型中每个节点和自由度的存在。