比较租金流现值和仪器现值：应该购买还是租赁

1.由边际函数求总量函数

由于总量函数（如总成本、总收益、总利润等）的导数就是边际函数、（如边际成本、边际收益、边际利润等），当已知初始条件时，即可用定积分求出总量函数，在经济活动中经常遇到的求总量问题，有以下几类：

（1）已知某产品的边际成本为C′（x）（x表示产量），固定成本C（0），则总成本函数为

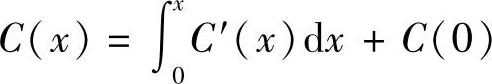
产量从a增到b（a＜b）的总成本为

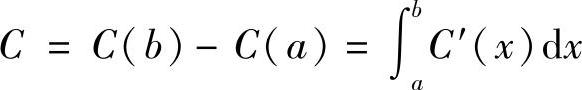
（2）已知某产品的边际收入为R′（x）（x表示销量），则销售x个产品的总收入函数

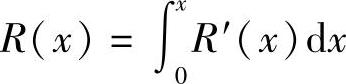
销量从a增到b时的总收入为

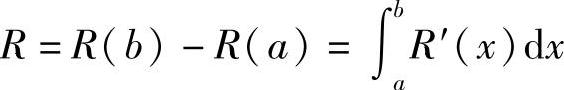
总收入扣除总成本为利润，所以边际利润=边际收入-边际成本.若已知边际收入R（x₁）（x₁表示销量）、边际成本C′（x₂）（x₂表示产量），当全部产品无积压时（x₁=x₂=x），所获总利润为

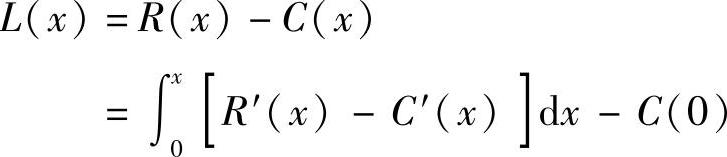
产量从a增加到b时所获总利润为

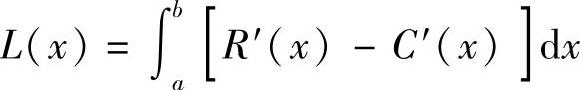
例7 已知生产某产品每台的成本为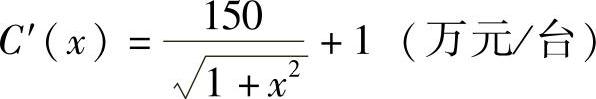，边际收入为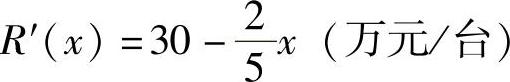.若固定成本为C（0）=10（万元），求：（1）总成本函数、总收入函数和总利润函数；（2）当产量从40台增加到80台时，其总成本与总收入的增量.

解 （1）总成本为固定成本与可变成本之和，于是，总成本函数为

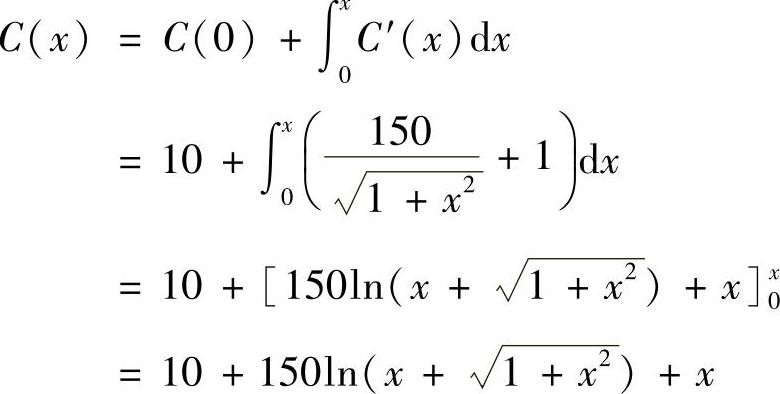
由于当产量为零时，总收入为零，即R（0）=0，于是总收益函数为

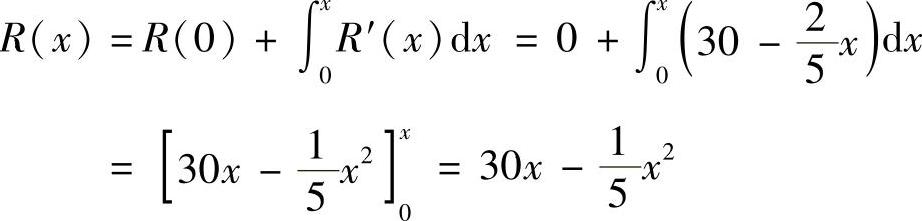
由于总利润为总收入与总成本之差，故总利润函数为

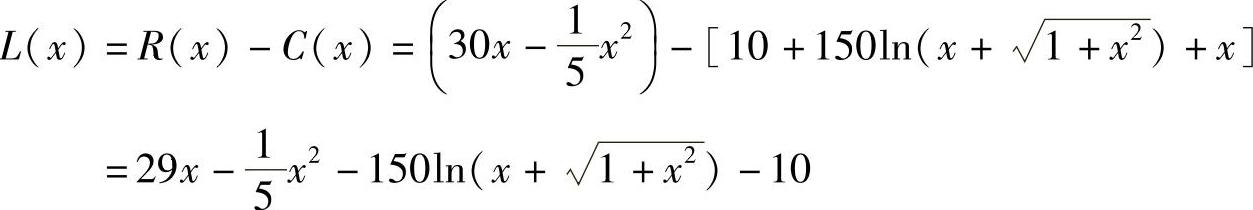
（2）当产量从40台增加到80台时，总成本的增量为

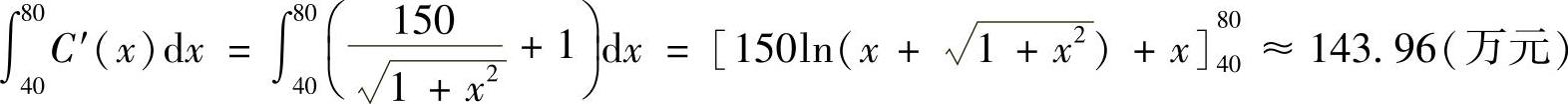
当产量从40台增加到80台时，总收入的增量为

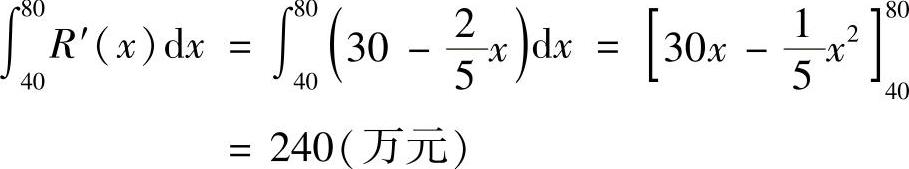
2.消费者剩余问题

需求函数Q=f（P）与供给函数Q=g（P）通常都是价格P的单调函数，设其反函数分别为P=f^-1（Q），P=g^-1（Q），如图6-32所示.

设反函数交点（Q^∗，P^∗）是针对某种商品而言的.这个交点是顾客愿意购买的价格，也是生产者愿意卖出的价格.如果消费者以比他们原来预期低的价格购买某种商品，由此而节省下来的钱称为消费者剩余.

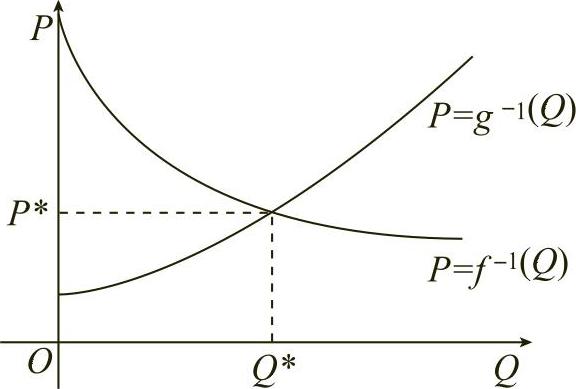
图6-32(https://www.xing528.com)

设购买点为Q^∗，则消费者剩余为区间[0，Q^∗]上的一个值v，下面用微元法来计算它.∀Q∈[0，Q^∗]，在区间[Q，Q+dQ]上的消费者剩余微元为

dv=f^-1（Q）dQ-P^∗dQ

=[f^-1（Q）-P^∗]dQ

从而消费者剩余为

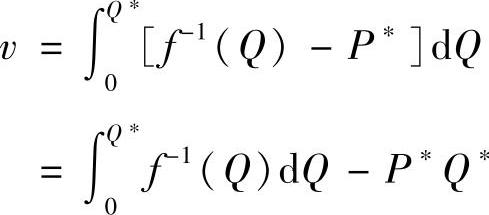
例8 设某产品的需求函数是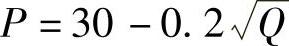，若价格固定在每件10元，求消费者剩余.

解 已知需求函数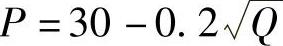，首先求出对应于P=10时的Q值，令30-0.2Q=10，得Q=10000，于是消费者剩余为

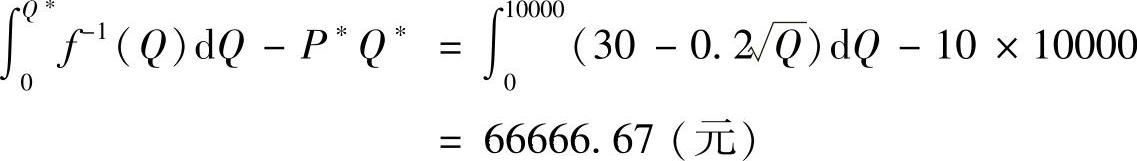
3 . 资本贬值与投资

若以年利率r进行复利计算，一笔A元的资金从现在起存入银行，则t年后的本利之和为Ae^rt元，那么称Ae^rt为A元资金在t年后的将来值.

如果t年末希望得到A元资金，且按年利率进行连续复利计算，那么现在需要投入资金Ae^-rt元，并称Ae^-rt为资金A的现值.

通常，支付给某人的款项或某人获得的款项是离散的支付或获得的，即在某一特定的时刻支付或获得的.但是对于一个大系统（如公司或企业），其收入与支出是随时流进和流出的，这些收入可以表示为连续的收入流或支出流.

设某企业在时间区间[0，T]上的收入流的变化率为f（t）（元/年或元/月），且年利率为r，将来值与现值是区间[0，T]上的一个值，下面用微元法计算.

∀t∈[0，T]，则在区间[t，t+dt]内资金的将来值的微元为

f（t）dt·e^r（T-t）=f（t）e^r（T-t）dt

从而将来值为

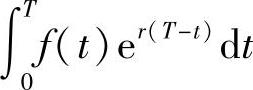
在区间[t，t+dt]内资金的现值的微元为

f（t）dt·e^-rt=f（t）e^-rtdt

从而现值为

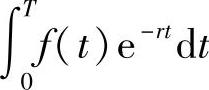
例9 某实验室准备采购一台仪器，其使用寿命为15年.这台仪器的现价为100万元，如果租用该仪器每月需要支付租金1万元，资金的年利率为5%，以连续复利计算.试判断是采购仪器合算还是租用仪器合算？

解 将15年租金的总值的现值与该仪器的现值进行比较，即可做出决策.租金流现值的总值为

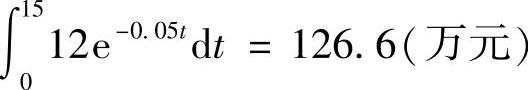
所以，与该仪器的现值100万元相比，还是采购仪器合算.

例10 一对夫妻准备为孩子存款积攒学费，目前银行的存款年利率为2%，以连续复利计算，若他们打算10年后攒够5万元，计算这对夫妻每年应等额地为其孩子存入多少钱？

解 这对夫妻每年应等额地为其孩子存入A元（即存款流为f（t）=A元），使得10年之后存款总额的将来值达到5万元，则

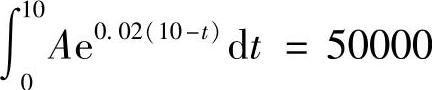
即有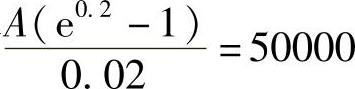，得到A=4517，即这对夫妻应每年等额存入4517元，10年后才能为孩子攒够5万元的学费.