【摘要】：1.直角坐标系中普通方程的情形设曲线C由方程y=f（x），x∈[a，b]给出，如图6-20所示，其中y=f（x）有连续的导数.任取x∈[a，b]，在区间[x，x+Δx]上对应的一小段弧长为则曲线C的弧长元素为从而所求弧长为图6-202.直角坐标系中参数方程的情形设曲线C由方程给出，其中x=x（t）y=y（t）在区间[α，β]上有连续的导数，则其长度为3.极坐标方程的情形设曲线C由极坐标方程ρ=ρ（
1.直角坐标系中普通方程的情形
设曲线C由方程
y=f（x），x∈[a，b]
给出，如图6-20所示，其中y=f（x）有连续的导数.任取x∈[a，b]，在区间[x，x+Δx]上对应的一小段弧长为
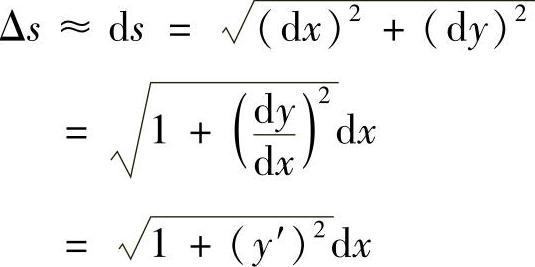
则曲线C的弧长元素为
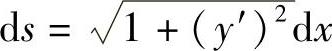
从而所求弧长为
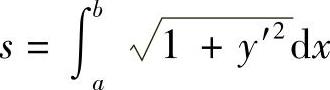
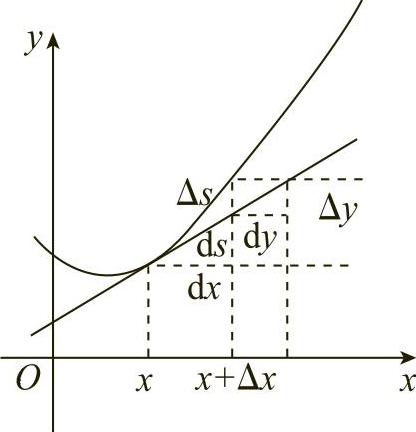
图6-20
2.直角坐标系中参数方程的情形
设曲线C由方程
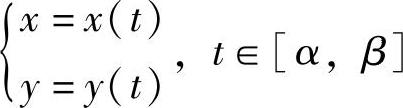
给出，其中x=x（t）y=y（t）在区间[α，β]上有连续的导数，则其长度为
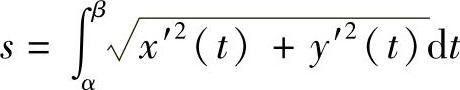
3.极坐标方程的情形
设曲线C由极坐标方程
ρ=ρ（θ），θ∈[α，β]
给出，其中ρ=ρ（θ）在区间[α，β]上有连续的导数.将方程由极坐标转换为直角坐标，且以θ为参变量的曲线方程是
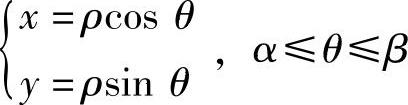
则(https://www.xing528.com)
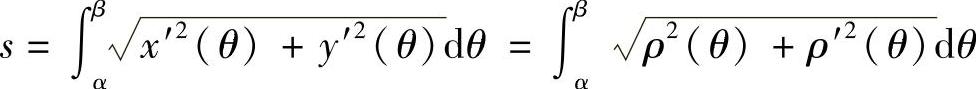
例1 求曲线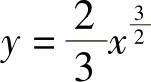
上相应于x从a到b的一段弧的长度（见图6-21）.
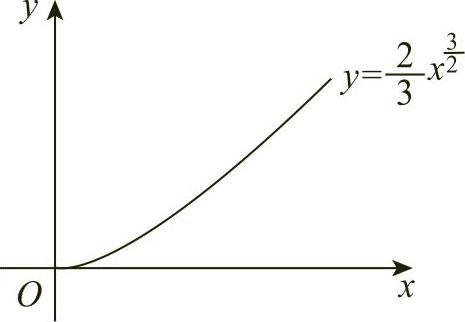
图6-21
解 由长度计算公式得
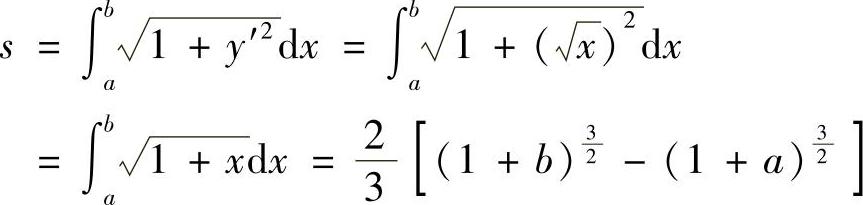
例2 求圆周x=rcost，y=rsint，t∈[0，2π]的弧长.
解 由长度计算公式得
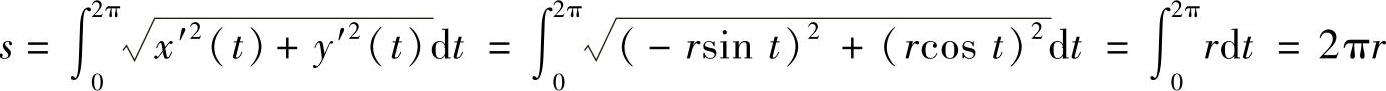
例3 求摆线
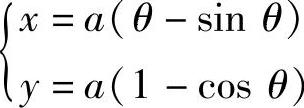
的一拱（0≤θ≤2π）的长度（见图6-22）.
解 因为
x′（θ）=a（1-cosθ），y′（θ）=asinθ
从而由长度计算公式得
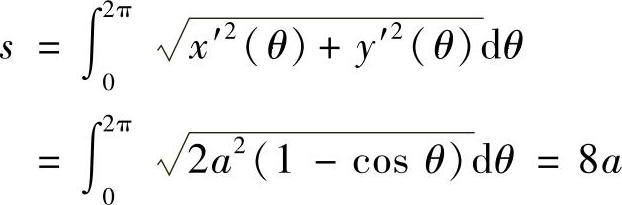
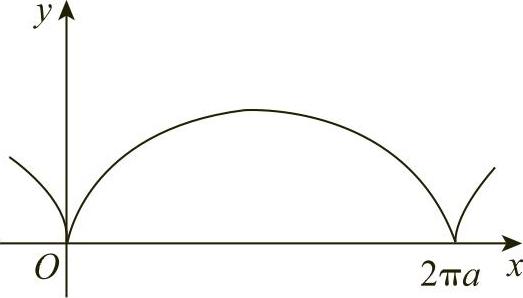
图6-22
例4 求阿基米德螺线ρ=aθ（a＞0）相应于θ从0到2π的一段弧长.
解 因为ρ′（θ）=a，则由长度计算公式得
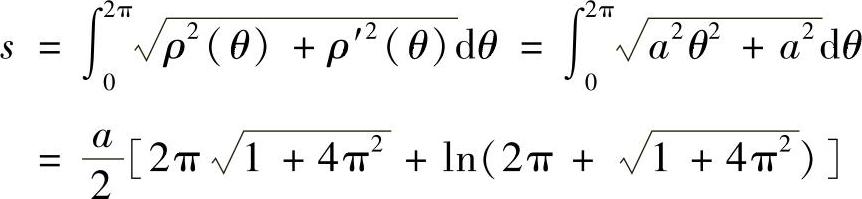
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
