【摘要】：定义2 由一个平面内的图形绕这个平面内某直线旋转一周而形成的立体称为旋转体，这条直线称为旋转轴.可见旋转体作为一类特殊的立体，其截面面积A（x）很容易求出，故其体积公式容易推出.设连续函数y=f（x），x∈[a，b]，旋转体是由平面图形0≤y≤f（x），x∈[a，b]绕x轴旋转一周而得（见图6-14），那么其在区间[a，b]上的截面面积函数为A（x）=π[f（x）]2则由公式得旋转体的体积图6-1
定义2 由一个平面内的图形绕这个平面内某直线旋转一周而形成的立体称为旋转体，这条直线称为旋转轴.
可见旋转体作为一类特殊的立体，其截面面积A（x）很容易求出，故其体积公式容易推出.
设连续函数y=f（x），x∈[a，b]，旋转体是由平面图形
0≤y≤f（x），x∈[a，b]
绕x轴旋转一周而得（见图6-14），那么其在区间[a，b]上的截面面积函数为
A（x）=π[f（x）]2
则由公式得旋转体的体积
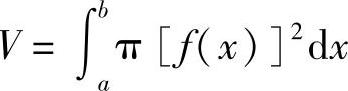
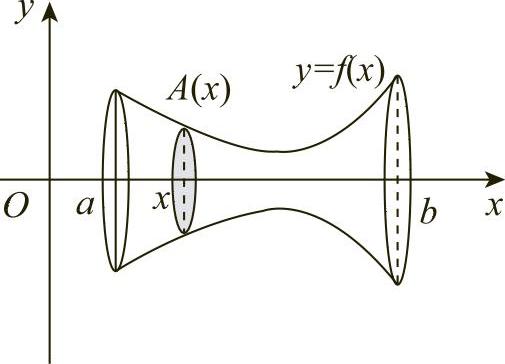
图6-14
同样可以得到由曲线x=φ（y），y=c，y=d（c＜d）及y轴围成的曲边梯形绕y轴旋转一周的旋转体（见图6-15）体积
V=∫dcπ[φ（y）]2dy
例3 求由椭圆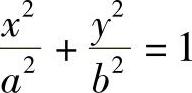
所围成的图形绕x轴旋转一周而成的旋转体的体积（见图6-16）.
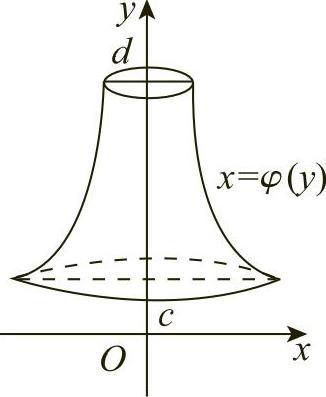
图6-15
解 该旋转体为上半椭圆(https://www.xing528.com)
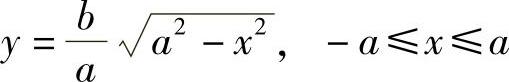
及x轴所围成的图形绕x轴旋转一周而围成的立体.故按旋转体体积公式有
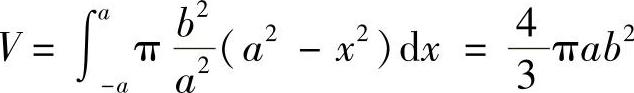
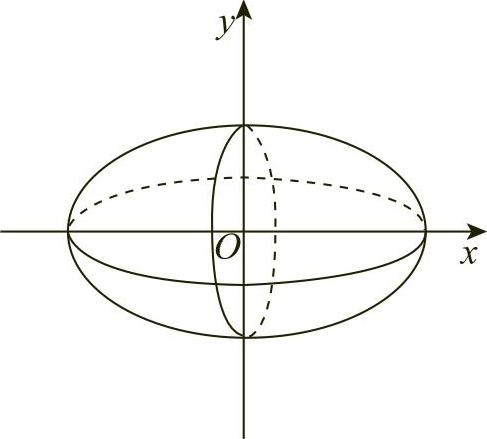
图6-16
例4 求由圆x2+（y-R）2≤r2（r＜R）绕x轴一周所得的旋转体的体积（见图6-17）.
解 该旋转体是一个圆环体.设圆x2+（y-R）2=r2的上、下半圆分别表示为
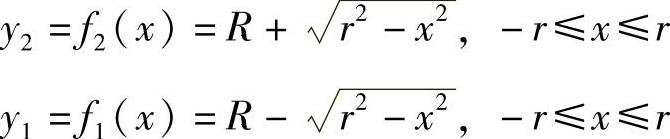
所以旋转体的截面面积函数为
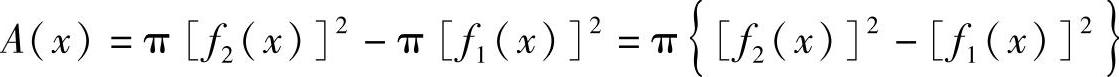
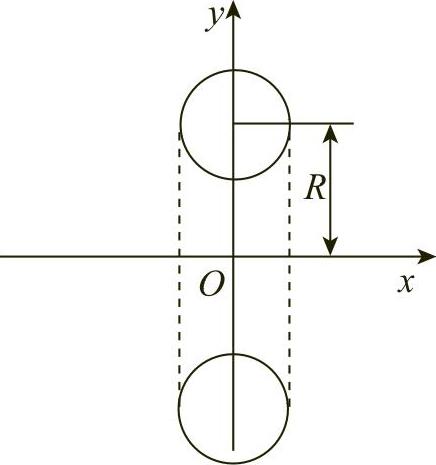
图6-17
利用体积的对称性以及旋转曲面的体积公式有
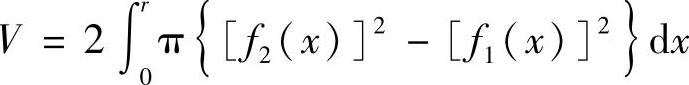
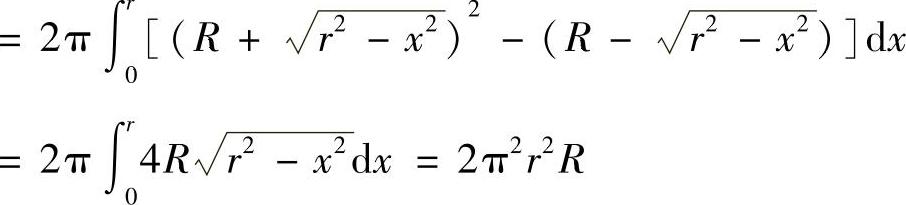
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
