【摘要】：定义1 设Ω为空间立体，如图6-11所示，它夹在垂直于x轴的两平面x=a与x=b（a＜b）之间，过任意一点x∈[a，b]构造垂直于x轴的平面去截Ω，则截得的面积为x的函数，记为A（x），x∈[a，b]，并称它为空间立体Ω的截面面积函数.下面用元素法导出由截面面积函数求空间立体体积的计算公式.设A（x）在区间[a，b]上连续，任意取x∈[a，b]，在区间[x，x+dx][a，b]上对应的体积元素为d
定义1 设Ω为空间立体，如图6-11所示，它夹在垂直于x轴的两平面x=a与x=b（a＜b）之间，过任意一点x∈[a，b]构造垂直于x轴的平面去截Ω，则截得的面积为x的函数，记为A（x），x∈[a，b]，并称它为空间立体Ω的截面面积函数.
下面用元素法导出由截面面积函数求空间立体体积的计算公式.
设A（x）在区间[a，b]上连续，任意取x∈[a，b]，在区间[x，x+dx]⊆[a，b]上对应的体积元素为
dV=A（x）dx
则立体Ω的体积为
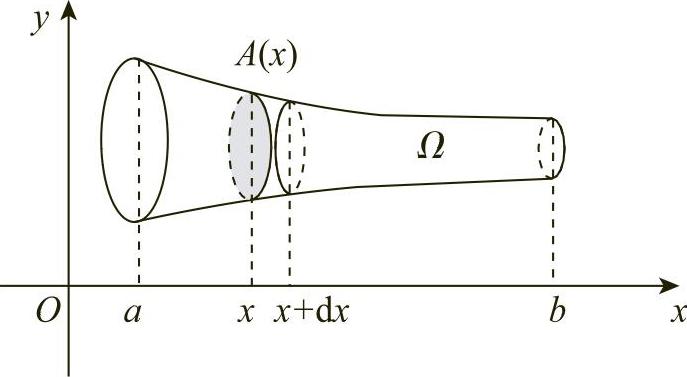
图6-11
例1 一平面经过半径为R的圆柱体的底圆中心，并与地面交成角α，计算这平面截圆柱体所围得的立体的体积（见图6-12）.
解 过x轴上的点x∈[-R，R]，且垂直于x轴的截面是一个直角三角形，故截面积为
则所求立体体积为
(www.xing528.com)
图6-12
例2 求以半径为R的圆为底、平行且等于底圆直径的线段为顶、高为h的正劈锥体的体积（见图6-13）.
解 取底圆所在平面为Oxy平面，圆心O为原点，x轴平行于正劈锥体的顶，则底面圆的方程为
x2+y2=R2
过x轴上的点x∈[-R，R]，垂直于x轴的截面是等腰三角形，其面积为
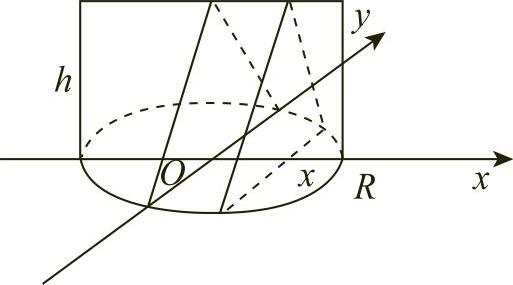
图6-13
则所求立体体积为
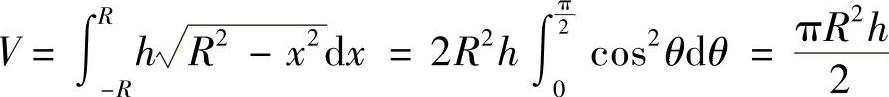
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
