在直角坐标系中计算-高等数学上

1.由曲线y=f（x），x=a，x=b（a＜b），x轴围成的区域的面积

如图6-2所示，由定积分的几何意义，如果y=f（x）≥0，则所围的面积为

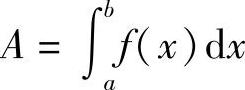
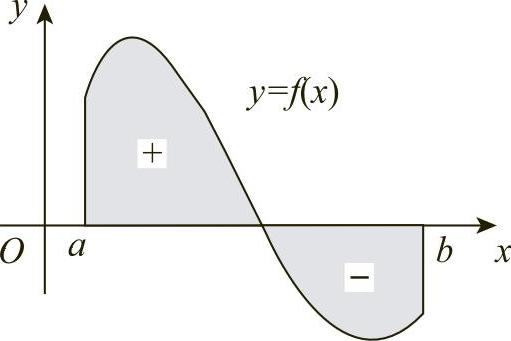
图6-2

若y=f（x）在区间[a，b]上不都是非负的，则所围的面积为

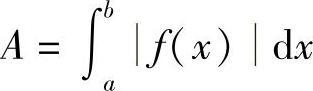
2.由曲线y=f₁（x），y=f₂（x），x=a，x=b（a＜b）所围成的区域（x-区域）的面积

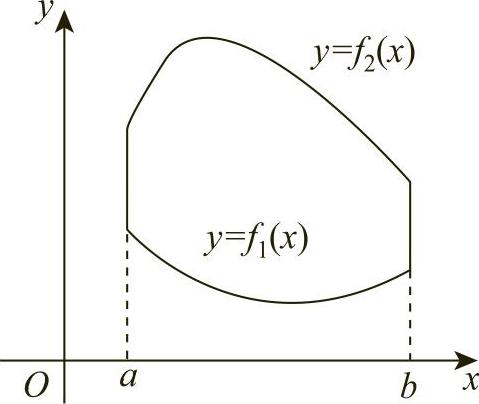
图6-3

如图6-3所示，围成的面积相应于在区间[a，b]上，由曲线f₁（x），f₂（x）所围成的区域的面积.在区间[a，b]上任一小区间[x，x+dx]上对应的面积元素为

dA=[f₂（x）-f₁（x）]dx

由元素法可得所围成的面积

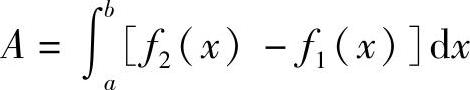
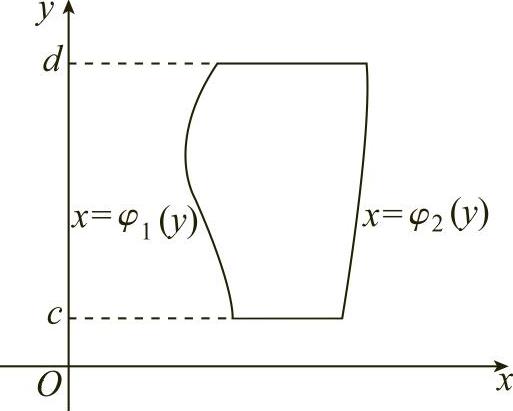
3.曲线x=φ₁（y），x=φ₂（y），y=c，y=d（c＜d）围成的区域（y区域）面积

如图6-4所示，围成的面积相应于在区间[c，d]上，由曲线φ₁（y），φ₂（y）所围成的区域的面积.在区间[c，d]上任一小区间[y，y+dy]上对应的面积元素为

dA=[φ₂（y）-φ₁（y）]dy

由元素法可得所围成的面积

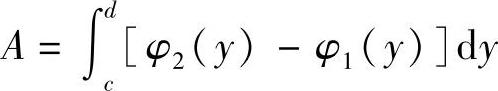
例1 求曲线y=x²，x=y²所围成的图形的面积（见图6-5）.

(https://www.xing528.com)

图6-4

解 解方程组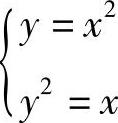，得到曲线的交点（0，0）及（1，1），于是

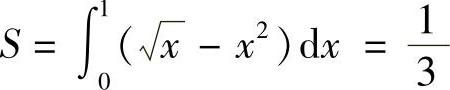
例2 求抛物线y²=2x与直线x+y=4所围成的图形的面积（见图6-6）.

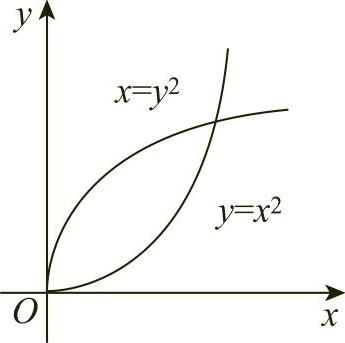
图6-5

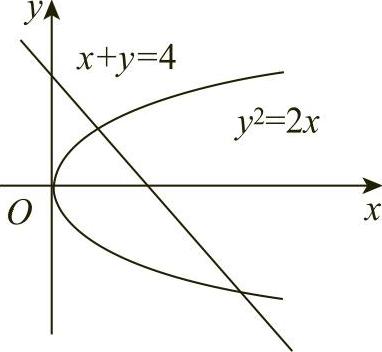
图6-6

解 方法一解方程组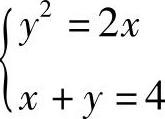，得交点（2，2），（8，-4）.将图形分割为两个x-型区域，有

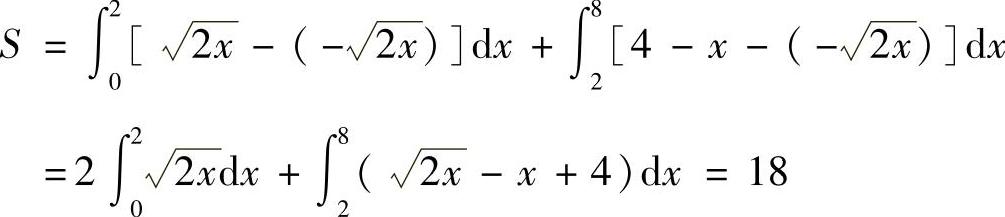
方法二 将图形看作y-区域，曲线方程写为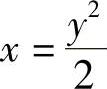，x=-y+4，有

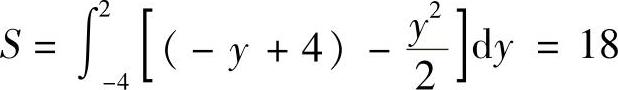
例3 求椭圆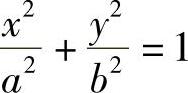所围成的图形的面积（见图6-7）.

解 设椭圆的参数方程为

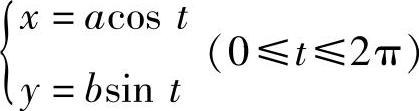
利用图形的对称性有

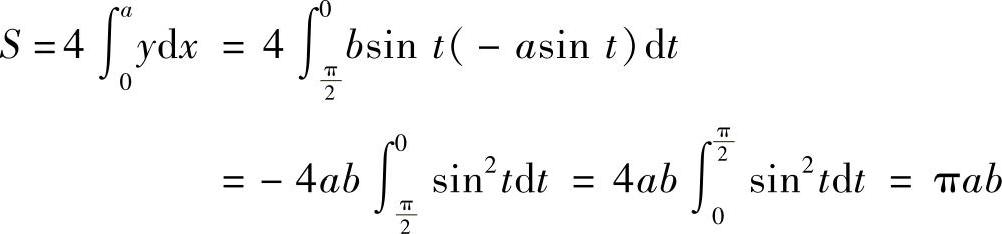
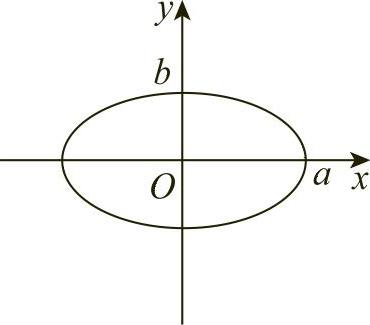
图6-7