高等数学上册：第二类换元法应用举例

1.三角代换

（1）被积函数中含有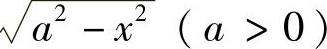，可令x=asint，并约定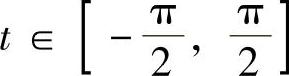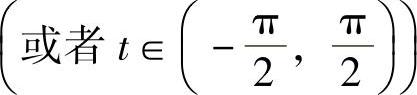，则

进而可将原积分化为三角有理函数的积分.

（2）被积函数中含有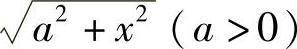，可令x=atant，并约定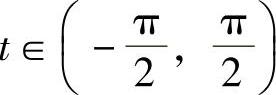，则

进而可将原积分化为三角有理函数的积分.

（3）被积函数中含有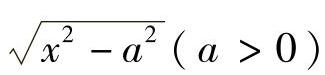，当x≥a时，可令x=asect，并约定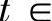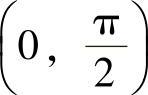，则

当x≤-a时，可令u=-x，则u≥a，进而可将原积分化为三角有理函数的积分.

例28 求.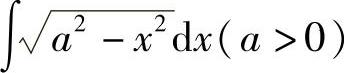

解 令x=asint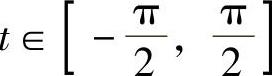，，则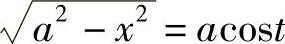，dx=acostdt，则

例29 求.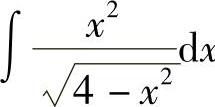

解 令x=2sint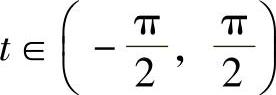，，则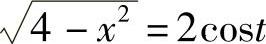，dx=2costdt，则

例30 求.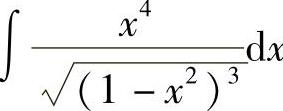

解 令x=sint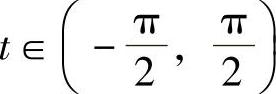，，则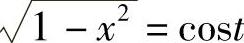，dx=costdt，则

例31 求.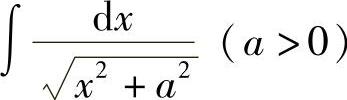

解 令x=atant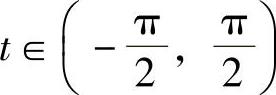，，则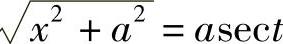，dx=asec²tdt

例32 求.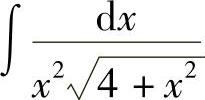

解 令x=2tant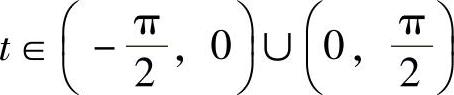，则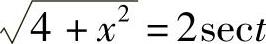，dx=2sec²tdt，则

例33 求.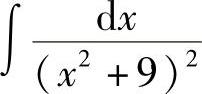

解 令x=3tant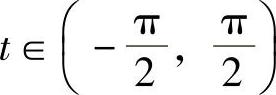，，则x²+9=9sec²t，dx=3sec²tdt，则

例34 求.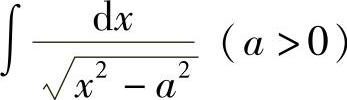

解 被积函数的定义域为（-∞，-a）∪（a，+∞），当x∈（a，+∞）时，令x=asect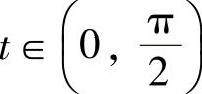，，则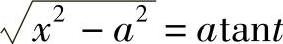，dx=asecttantdt，则

当x∈（-∞，-a）时，令u=-x，则u∈（a，+∞），有

则当x∈（-∞，-a）∪（a，+∞）时，

例35 求.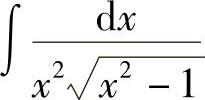

解 当x∈（1，+∞）时，令x=sect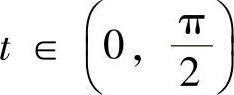，，则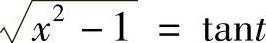，dx=secttantdt，有

当x∈（-∞，1）时，令u=-x，则u∈（1，+∞），有

则无论x＜-1还是x＞1，均有

注意：（1）以上三种三角代换，目的是将无理式积分化为三角有理函数积分.

（2）在将积分结果化为x的函数时，常常用到同角三角函数的关系，其中一种较简单和直接的方法是用“辅助三角形”.

（3）在既可用第一类换元法也可用第二类换元法时，用第一类换元法可使计算更为简捷.(www.xing528.com)

例36 求.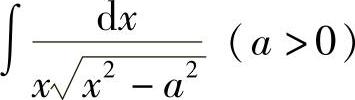

解 显然，此题可以用第二类换元法，但若用第一类换元法，将简单得多.当x＞a时，有

当x＜-a时，令u=-x，则u＞a，有

两式合写有

2.有理根式积分

含根式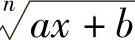的函数的积分，可令，进而化为有理函数的积分.

例37 求.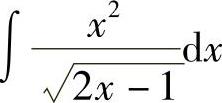

解 令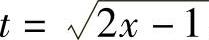，即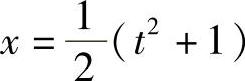，dx=tdt，则

例38 求.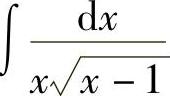

解 令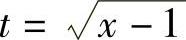，即x=t²+1，dx=2tdt，则

例39 求.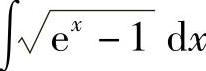

解 令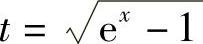，即x=ln（t²+1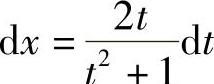），，则

当被积函数含有两种或两种以上的根式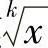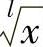，…，时，可令x=tⁿ，其中n为各根指数的最小公倍数，进而化为有理分式的积分.

例40 求.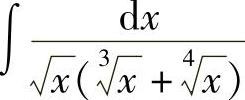

解 显然为了使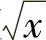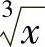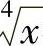，，都变成有理式，应令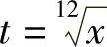，则

3.三角有理函数的积分

在这种情况下可采用万能代换，即令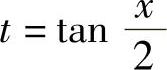，x∈（-π，π），则

例41 求.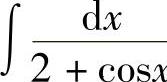

解 令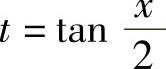，则

例42 求.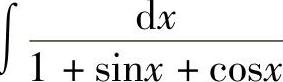

解 令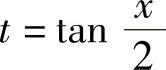，则

4.分母的阶较高的函数的积分

在这种情况下可令.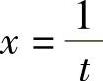

例43 求.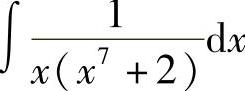

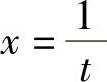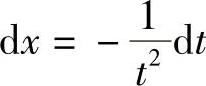解 令，即，则

例44 求.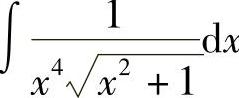

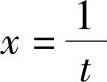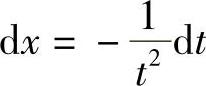解 令，即，则

除前面的基本积分外，还有一些常用积分.