高数上册：第一类换元法应用实例

例1 求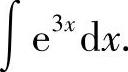

解 e^3x是一个复合函数，设中间变量u=3x，则du=d（3x）=3dx，即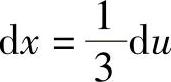，则

例2 求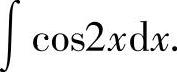

解 令u=2x，则du=2dx，则

例3 求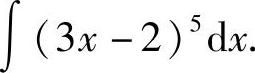

解 设u=3x-2，则du=3dx，则

在计算中，如果不写出中间变量u，在被积表达式中直接凑出一个函数的微分，即中间变量u的微分，进而求出微分的方法称为凑微分法.如上述例3可以这样解：

常见的凑微分形式有：

例4 求.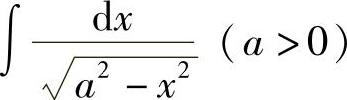

解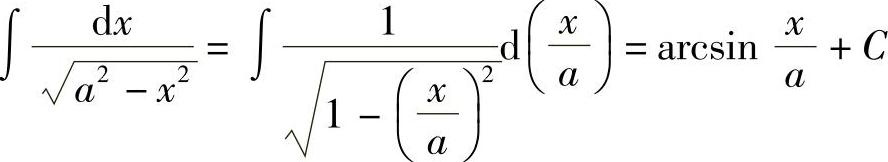

例5 求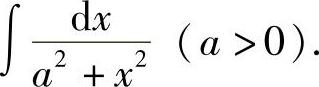

解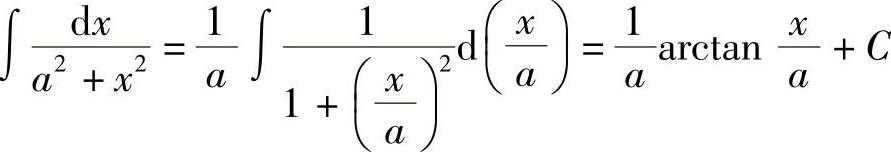

例6 求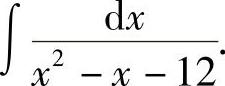

解 因为

所以

例7 求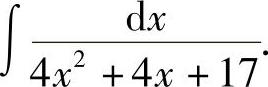

解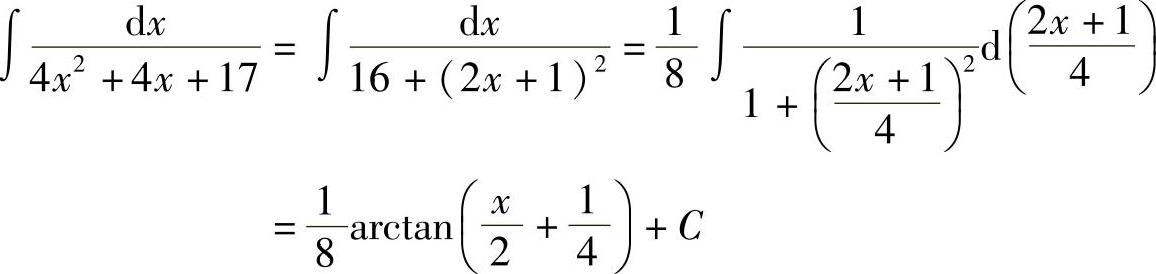

例8 求.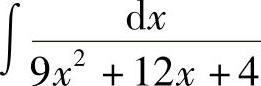

解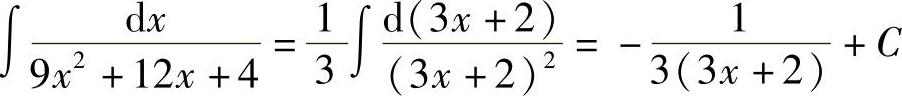

注意：在例6、例7、例8中，当被积函数的分母是二次三项式时，可以按照根的不同情况采用不同的处理方法.除了以上类型，还可以利用d（xⁿ）=nx^n-1dx.看下面的例题：

例9 求.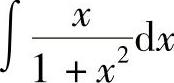

解 由d（x²+1）=2xdx，即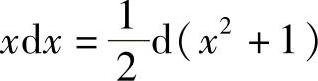，则

例10 求.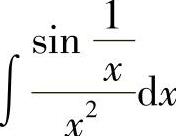

解 由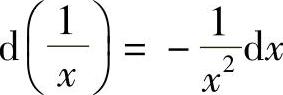，得

例11 求.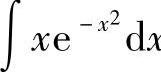

解 由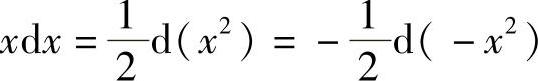，得

例12 求.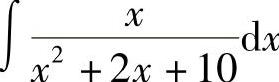

解 由

得

利用d（e^x）=e^xdx，d（a^x）=a^xlnadx，则有以下应用：

例13 求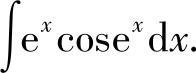

解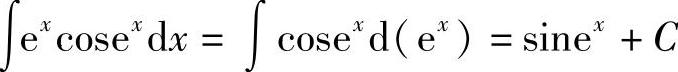

例14 求.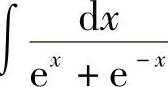

解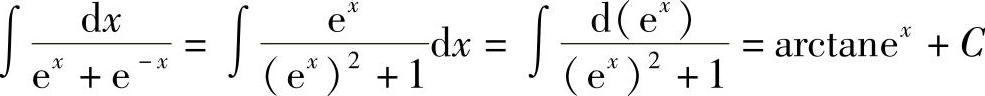

例15 求.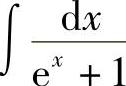

解 因为(https://www.xing528.com)

则

例16 求.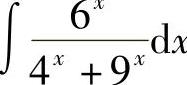

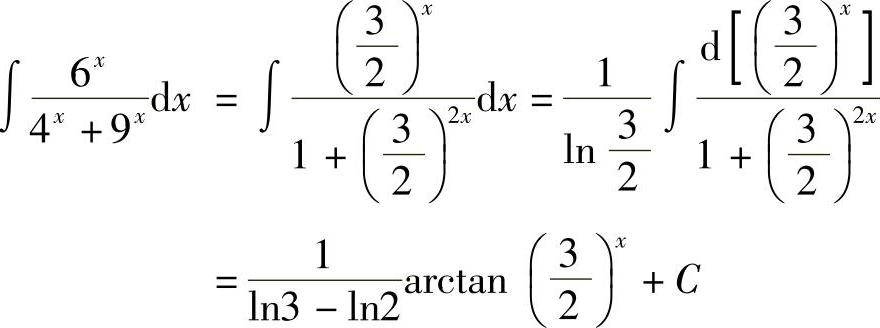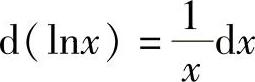解利用，有以下应用.

例17 求.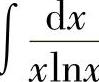

解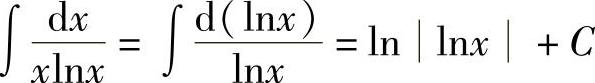

例18 求.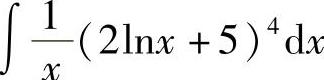

解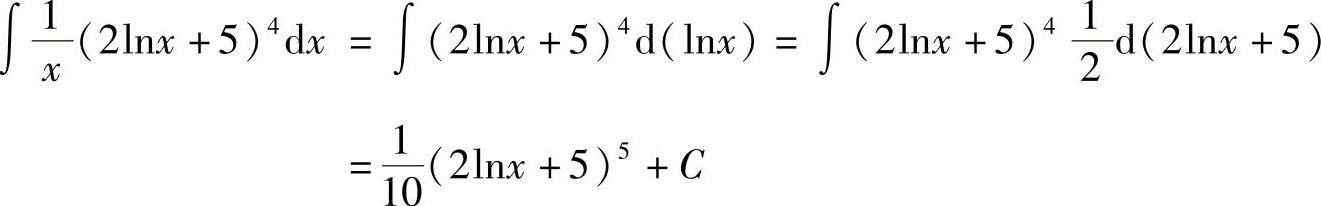

利用三角函数的微分公式：

d（sinx）=cosxdx，d（cosx）=-sinxdx，d（tanx）=sec²xdx，d（cotx）=-csc²xdx则有以下应用：

例19 求∫tanxdx.

解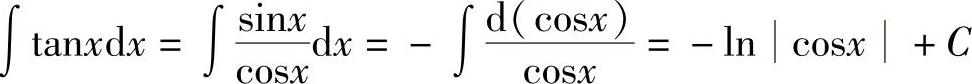

例20 求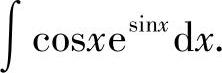

解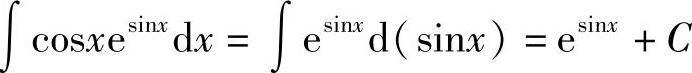

例21 求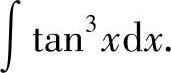

解 方法一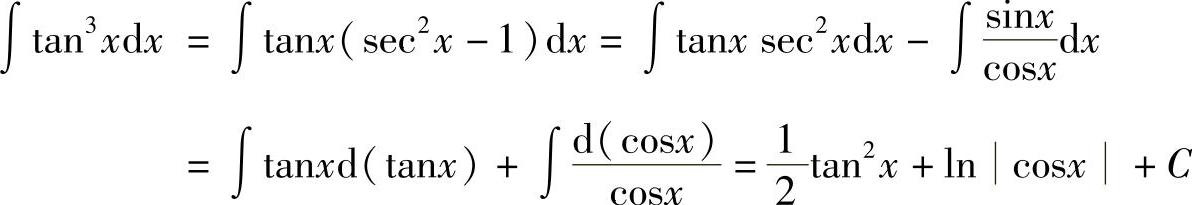

方法二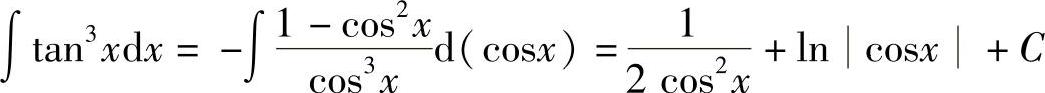

例22 求.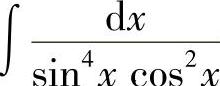

解 因为

所以

利用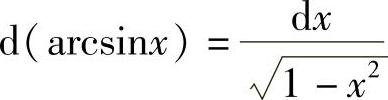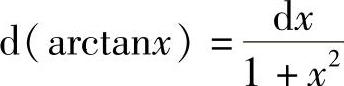，，有以下应用：

例23 求.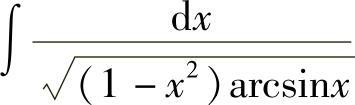

解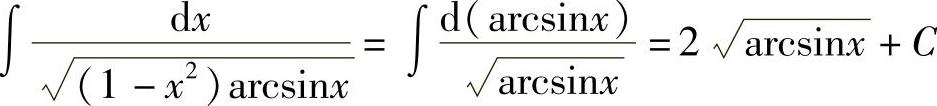

例24 求.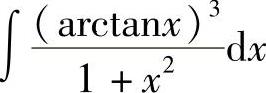

解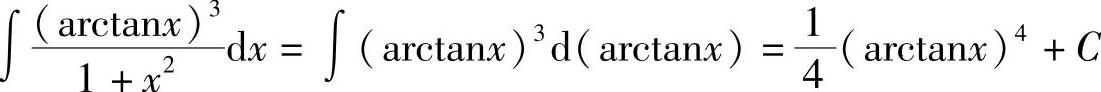

由以上例题可以看出，第一类换元法是一种非常灵活的计算方法，始终具有“逆向思维”的特点.因此对初学者来讲，较难适应，学生应熟悉这些基本例题.当然也有一些题，它不属于这些基本题型，但我们也可以通过观察找到解题的途径.

例25 求.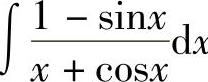

解 注意到d（x+cosx）=（1-sinx）dx，则

例26 求∫.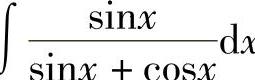

解 因为

所以

例27 求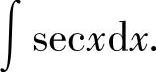

解 方法一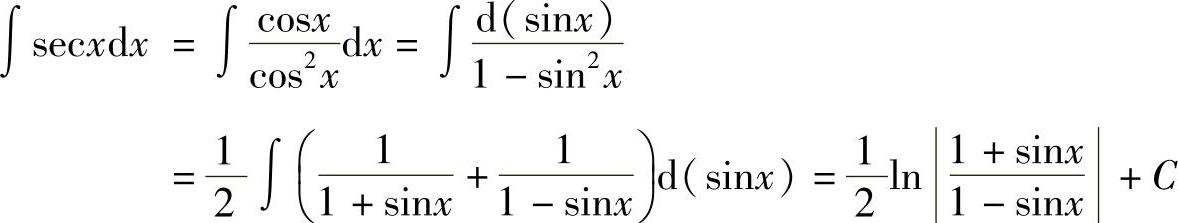

方法二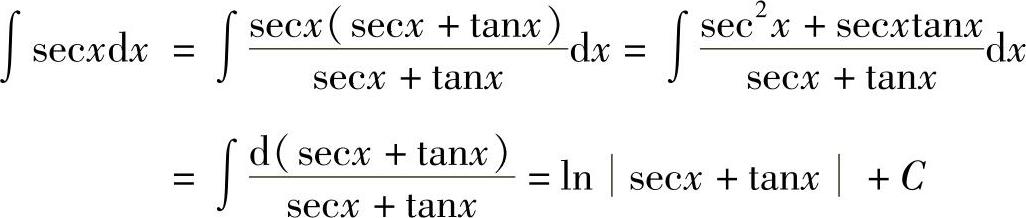

同样的方法可以求得