我们认识到:直线不弯曲,半径较小的圆弯曲得比半径较大的圆厉害些,而其他曲线有不同的弯曲程度.例如,抛物线y=x2在顶点附近弯曲得比远离顶点的部分厉害些.
下面讨论如何用数量来描述曲线的弯曲程度.
在图3-16中可以看出,弧段 比较平直,当动点沿这段弧从M1移动到M2时,切线转过的角度φ1不大;而弧段
比较平直,当动点沿这段弧从M1移动到M2时,切线转过的角度φ1不大;而弧段 弯曲得比较厉害,角φ2就比较大.
弯曲得比较厉害,角φ2就比较大.
但是,切线转过角度的大小还不能完全反映曲线弯曲的程度.例如,从图3-17中可以看出,两端曲线弧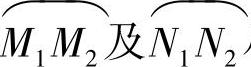 尽管其切线转过的角度都是φ,然而弯曲程度并不相同:短弧段比长弧段弯曲得厉害些.由此可见,曲线弧的弯曲程度还与弧段的长度有关.
尽管其切线转过的角度都是φ,然而弯曲程度并不相同:短弧段比长弧段弯曲得厉害些.由此可见,曲线弧的弯曲程度还与弧段的长度有关.

图3-16

图3-17
按上面的分析,下面给出描述曲线弯曲程度的曲率概念.
设曲线C是光滑的,在曲线C上选定一点M0作为度量弧s的基点,设曲线上点M对应于弧s,在点M处切线的倾角为α(这里假定曲线C所在的平面上已设立了Oxy坐标系).曲线上另一点M′对应于弧s+Δs,在点M′处切线的倾角为α+Δα(见图3-18),那么,弧段 的长度为Δs,当动点从M移动到M′时切线转过的角度为Δα.
的长度为Δs,当动点从M移动到M′时切线转过的角度为Δα.
我们用比值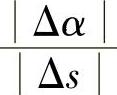 ,即单位弧段上切线转过的角度的大小来表达弧段
,即单位弧段上切线转过的角度的大小来表达弧段 的平均弯曲程度,把这比值叫作弧段
的平均弯曲程度,把这比值叫作弧段 的平均曲率,并记作
的平均曲率,并记作 ,即
,即 .类似于从平均速度引进瞬时速度的方法,当Δs→0时(即M′→M时),上述平均曲率的极限叫作曲线C在点M处的曲率,记作K,即
.类似于从平均速度引进瞬时速度的方法,当Δs→0时(即M′→M时),上述平均曲率的极限叫作曲线C在点M处的曲率,记作K,即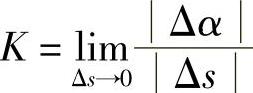 .
.
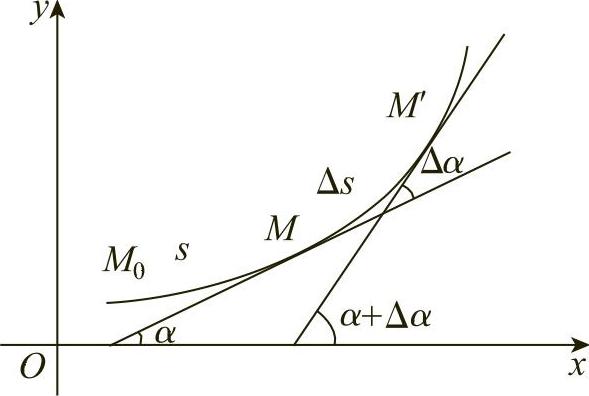
图3-18
在 存在的条件下,K也可以表示为
存在的条件下,K也可以表示为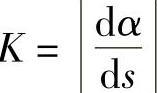 .
.
下面通过两个具体的例子来探讨曲率对弯曲程度的描述.
对直线来说,切线与直线本身重合.当点在直线上移动时,切线的倾角α不变,即Δα=0, ,从而
,从而 .这就是说,直线上任意点M处的曲率都等于零,这与我们认识到的“直线不弯曲”一致.
.这就是说,直线上任意点M处的曲率都等于零,这与我们认识到的“直线不弯曲”一致.
设圆的半径为r,在点M,M′处圆的切线所夹角Δα等于中心角∠MDM′.但
 ,于是
,于是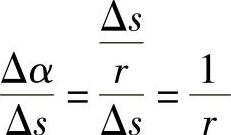 从而
从而
因为点M是圆上任意取定的一点,则上述结论表示圆上各点处的曲率都等于半径r的倒数 .这就是说,圆的弯曲程度每处都一样,且半径越小曲率越大,即弯曲得越厉害.
.这就是说,圆的弯曲程度每处都一样,且半径越小曲率越大,即弯曲得越厉害.
下面根据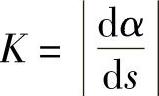 来导出便于实际计算的曲率的公式.(https://www.xing528.com)
来导出便于实际计算的曲率的公式.(https://www.xing528.com)
设曲线的直角坐标方程是y=f(x),且f(x)具有二阶导数(这时f′(x)连续,从而曲线是光滑的).因为tanα=y′,所以 ,即
,即
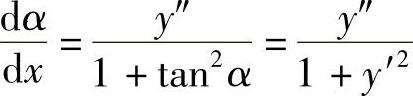
于是
又由 ,可得
,可得

若曲线由参数方程 给出,则曲线的曲率公式为
给出,则曲线的曲率公式为
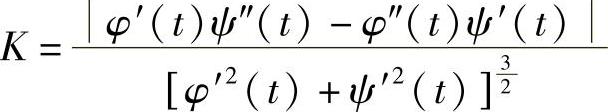
例1 计算等边双曲线xy=1在点(1,1)处的曲率.
解 由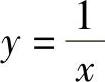 ,得
,得 ,
,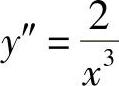 .因此,y′∣x=1=-1,y″∣x=1=2.把它们代入公式,便得曲线xy=1在点(1,1)处的曲率
.因此,y′∣x=1=-1,y″∣x=1=2.把它们代入公式,便得曲线xy=1在点(1,1)处的曲率

例2 抛物线y=ax2+bx+c上哪一点处的曲率最大?
解 由y=ax2+bx+c,得y′=2ax+b,y″=2a.代入公式,得

因为K的分子是常数2a,所以只要分母最小,K就最大.容易看出,当2ax+b=0,即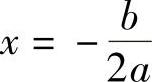 时,K的分母最小,因而K有最大值2a.而
时,K的分母最小,因而K有最大值2a.而 所对应的点为抛物线的顶点.因此,抛物线在顶点处的曲率最大.
所对应的点为抛物线的顶点.因此,抛物线在顶点处的曲率最大.
在有些实际问题中,∣y′∣同1比较起来是很小的(有的工程技术书上记为∣y′∣≪1),可以忽略不计.这时,由1+y′2≈1,则曲率的近似计算公式为

这就是说,当∣y′∣≪1时,曲率K近似于∣y″∣.经过这样简化之后,对一些复杂问题的计算和讨论就方便多了.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




