函数图形描绘的步骤与应用

借助于一阶导数f′（x）可以确定曲线的升降性和极值点；借助于二阶导数f″（x）可以确定曲线的凹凸性与拐点；再加上变化趋势，就可以确定函数的图形.所谓变化趋势一般有水平渐近线、垂直渐近线和无穷趋势三种.

现在我们可以应用前面所学的知识来描绘函数的图形，具体步骤如下：

（1）确定f（x）的定义域D，讨论其奇偶性及周期性；

（2）求出使f′（x）=0，f″（x）=0的点，以及f′（x），f″（x）不存在的点和间断点x_i；

（3）以各x_i为分点，将D划分为若干个子区间，并列表讨论f′（x），f″（x）在各子区间内的符号，从而确定曲线f（x）在各子区间的升降性、凹凸性、极值和拐点；

（4）讨论曲线f（x）的渐近线及其他变化趋势；

（5）建立直角坐标系，描出曲线的几个特殊点，并构造图形.

例3 构造函数y=x³-3x²+6的图形.

解 （1）函数的定义域为（-∞，+∞），而y′=3x²-6x=3x（x-2），y″=6x-6=6（x-1）.

（2）令y′=0，得x₁=0，x₂=2；令y″=0，得x₃=1.

（3）单调性、凹凸性、极值和拐点列表如下：

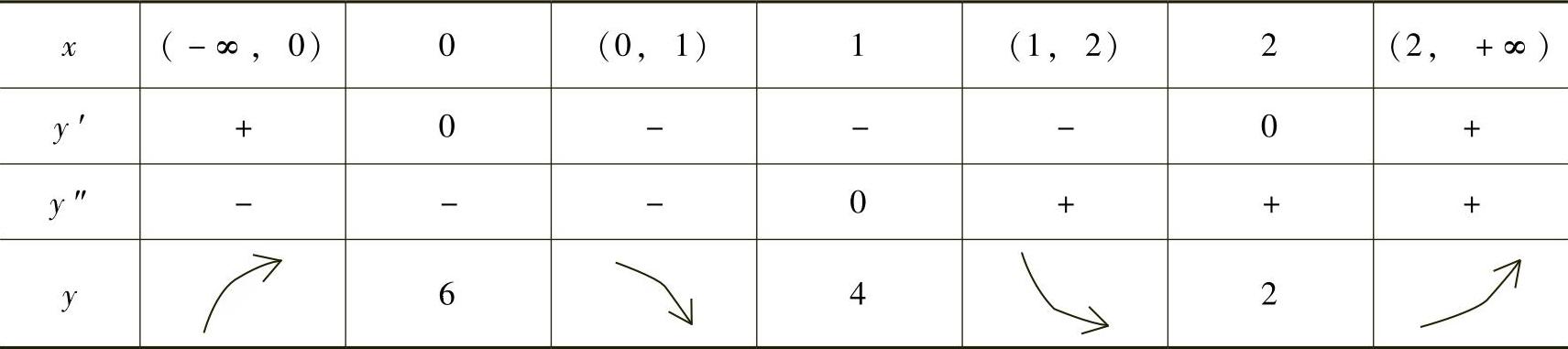
（4）变化趋势为：当x→-∞时，y→-∞；当x→+∞时；y→+∞；

（5）描点：A（0，6），B（1，4），C（2，2）.为了确定函数在区间（-∞，0）和（2，+∞）的图形，需要增加辅助作图点D（-1，2），E（3，6）.(www.xing528.com)

画出函数的图形，如图3-13所示.

例4 构造函数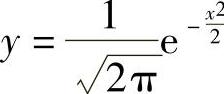的图形.

图3-13

解 （1）函数的定义域为（-∞，+∞），而，.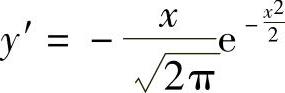

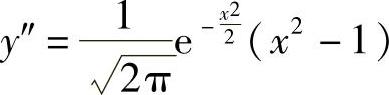（2）令y′=0，得x₁=0，令y″=0，得x₂=1，x₃=-1.

（3）单调性、凹凸性、极值和拐点列表如下：

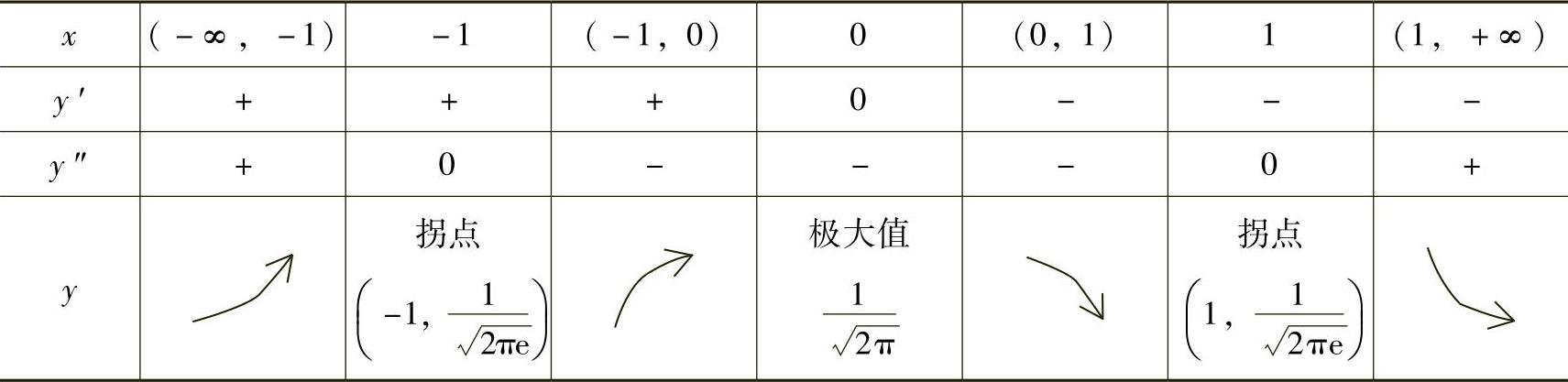
（4）变化趋势：因为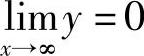，所以水平渐近线y=0；

（5）描点：，，.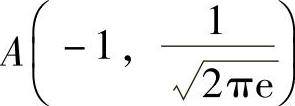

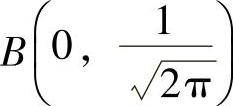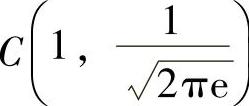画出函数的图形，如图3-14所示.

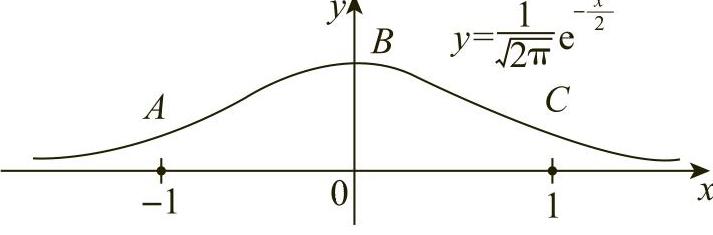
图3-14