函数f（x）=2x3-9x2+12x-3的单调性

在上节例4中我们看到，x=1及x=2是函数f（x）=2x³-9x²+12x-3的单调区间的分界点.例如，在x=1的左侧邻域，函数f（x）是单调增加的；在x=1的右侧邻域，函数f（x）是单调减少的.因此，存在x=1的一个去心邻域，对于去心邻域内的任何一点x，f（x）＜f（1）均成立.类似地，关于x=2，也存在一个去心邻域，对于去心邻域内的任何点x，f（x）＞f（2）均成立（见图3-5）.具有这种性质的点如x=1及x=2，在应用上有着重要的意义，值得我们对此进行一般性的讨论.

定义 设函数f（x）在区间（a，b）内有定义，x₀是区间（a，b）内的一个点.如果对于点x₀的一个去心邻域内的任何一点x，f（x）＜f（x₀）均成立，则称f（x₀）是函数f（x）的一个极大值；如果对于点x₀的一个去心邻域内的任何点x，f（x）＞f（x₀）均成立，则称f（x₀）是函数f（x）的一个极小值.

函数的极大值与极小值统称为函数的极值，使函数取得极值的点称为极值点.例如，上节例4中的函数f（x）=2x³-9x²+12x-3有极大值f（1）=2和极小值f（2）=1，x=1及x=2是函数f（x）的极值点.

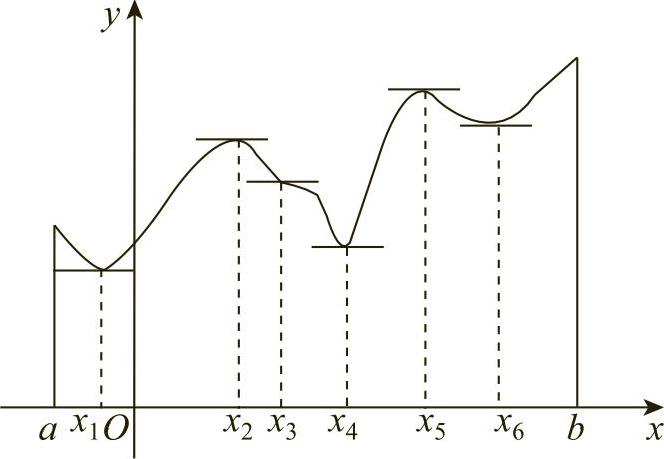
图3-7

函数的极值概念是局部性的.也就是说，如果f（x₀）是函数f（x）的一个极值，它只是在点x₀的一个局部范围内，并不一定是f（x）的整个定义域的最值.这一点一定要和函数的最值加以区分.

在图3-7中，函数f（x）有两个极大值f（x₂），f（x₅）；三个极小值f（x₁），f（x₄），f（x₆），其中极大值f（x₂）比极小值f（x₆）还小.就整个区间[a，b]来说，只有一个极小值f（x₁）同时是最小值，而没有一个极大值是最大值.

从图3-7还可以看到，在可导函数取得极值处，曲线上的切线是水平的.但曲线上有水平切线的地方，函数不一定取得极值.例如，图37中x=x₃处，曲线上有水平切线，但f（x₃）不是极值.

下面讨论函数取得极值的必要条件和充分条件.

定理1 （必要条件）设函数f（x）在点x₀处可导，且在x₀处取得极值，那么函数在点x₀处的导数为零，即f′（x₀）=0.

使导数为零的点（即方程f′（x₀）=0的实根）叫作函数的驻点.定理1是说：可导函数f（x）的极值点必定是它的驻点.但反过来，函数的驻点却不一定是极值点.例如，f（x）=x³的导数f′（x）=3x²，f′（0）=0，因此x=0是这个可导函数的驻点，但x=0却不是这个函数的极值点.因此，当求出了函数的驻点后，还需要判定求得的驻点是不是极值点.如果是的话，还要判断函数在该点究竟取得极大值还是极小值.下面利用定理2来判定函数的极值.

定理2 （第一充分条件）设函数f（x）在点x₀的一个邻域内可导，且f′（x₀）=0.

（1）如果当x取x₀左侧邻近的值时，f′（x）恒为正；当x取x₀右侧邻近的值时，f′（x）恒为负，那么函数f（x）在点x₀处取得极大值；

（2）如果当x取x₀左侧邻近的值时，f′（x）恒为负；当x取x₀右侧邻近的值时，f′（x）恒为正，那么函数f（x）在点x₀处取得极小值；

（3）如果当x取x₀左右两侧邻近的值时，f′（x）恒为正或负，那么函数f（x）在点x₀处没有极值.

具体情况如图3-8所示.

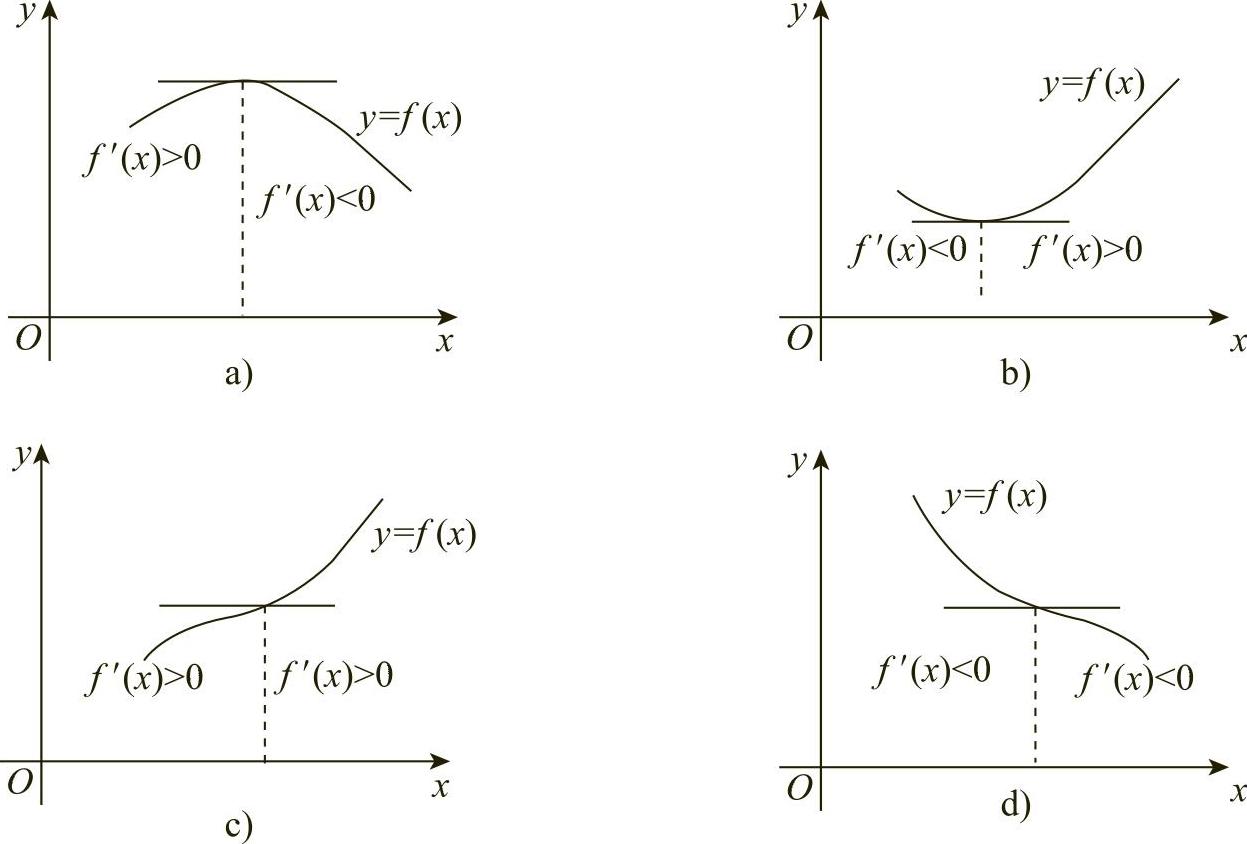
图3-8

根据上面的两个定理，如果函数y=f（x）在所讨论的区间内各点处都具有导数，就可以按下列步骤来求y=f（x）的极值点和极值：

（1）求出导数f′（x）；

（2）求出y=f（x）的全部驻点（即求出方程f′（x）=0在所讨论区间内的全部实根）；

（3）考察f′（x）的符号在每个驻点的左右邻域的情形，以便确定该驻点是否是极值点.如果是极值点，还要按定理2确定对应的函数值是极大值还是极小值；

（4）求出各极值点处的函数值，即得函数y=f（x）的全部极值.

例1 求出函数f（x）=x³-3x²-9x+5的极值.

解 （1）f′（x）=3x²-6x-9=3（x+1）（x-3）.

（2）令3（x+1）（x-3）=0，求得驻点x₁=-1，x₂=3.(www.xing528.com)

（3）由f′（x）=3（x+1）（x-3）来确定f′（x）的符号：

当x在-1的左侧邻域时，x+1＜0，x-3＜0，所以f′（x）＞0；当x在-1的右侧邻域时，x+1＞0，x-3＜0，所以f′（x）＜0.因而函数f（x）在x=-1处取得极大值.

同理，函数在x₂=3处取得极小值.

（4）算出极大值：f（-1）=10；极小值：f（3）=-22.

当函数y=f（x）在驻点处的二阶导数存在且不为零时，也可以利用下列定理来判定y=f（x）在驻点处取得极大值还是极小值.

定理3 （第二充分条件）设函数y=f（x）在点x₀处具有二阶导数，且f′（x₀）=0，f″（x₀）≠0，那么

（1）当f″（x₀）＜0时，函数f（x）在点x₀处取得极大值；

（2）当f″（x₀）＞0时，函数f（x）在点x₀处取得极小值.

证明请同学们自行探讨.

定理3 表明，如果函数f（x）在驻点x₀处的二阶导数f″（x₀）≠0，那么该驻点x₀一定是极值点，并且可以按二阶导数f″（x）的符号来判断f（x₀）是极大值还是极小值.但如果f″（x₀）=0，定理3就不能应用.事实上，当f′（x₀）=0，f″（x₀）=0时，f（x）在点x₀处可能有极大值，也可能有极小值，也可能没有极值.例如，f₁（x）=-x⁴，f₂（x）=x⁴，f₃（x）=x³这三个函数在x=0处就分别属于这三种情况，因此，如果函数y=f（x）在驻点处的二阶导数为零，那么还得用一阶导数在驻点左右邻域的符号来判断.

例2 求函数f（x）=（x²-1）³+1的极值.

解 （1）f′（x）=6x（x²-1）².

（2）令f′（x）=6x（x²-1）²=0，求得驻点x₁=-1，x₂=0，x₃=1.

（3）f″（x）=6（x²-1）（5x²-1）.

（4）因f″（0）=6＞0，f（x）在x=0处取得极小值，极小值为f（0）=0.

（5）因f″（-1）=f″（1）=0，用定理3无法判别.考察一阶导数f′（x）在驻点x₁=-1及x₃=1左右邻域的符号：

当x取-1左侧邻近的值时，f′（x）＜0；当x取-1右侧邻近的值时，f′（x）＜0；因为f′（x）的符号没有改变，所以f（x）在x=-1处没有极值.同理，f（x）在x=1处也没有极值（见图3-9）.

例3 求函数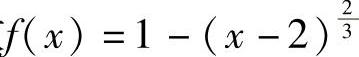的极值.

解 当x≠2时，.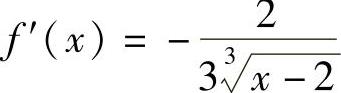

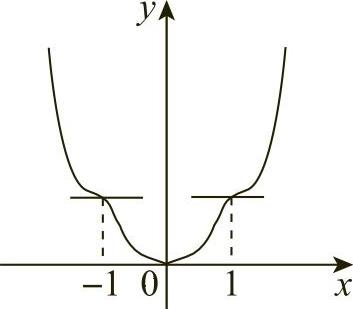
图3-9

当x=2时，f′（x）不存在.因此，当x≠2时，即在区间（-∞，2）和区间（2，+∞）内的各点处，f′（x）都存在，且f′（x）≠0.那么f（x）在这两个区间内没有极值点.事实上，在区间（-∞，2）内，f′（x）＞0，函数f（x）单调增加；在区间（2，+∞）内，f′（x）＜0，函数f（x）单调减少.

当x=2时，f′（x）不存在，但函数f（x）在该点连续，再由上面得到的函数的单调性可知，f（2）=1是函数f（x）的极大值.函数的图形如图3-10所示.

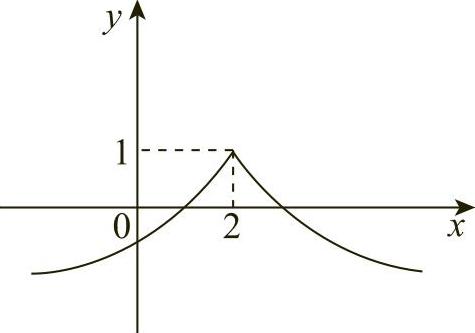
图3-10