罗尔定理中f（a）=f（b）这个条件相当特殊，如果把f（a）=f（b）这个条件取消，其余条件保留就得到了微分学中的重要的拉格朗日中值定理.
定理3 （拉格朗日中值定理）如果函数f（x）在闭区间[a，b]上连续，在开区间（a，b）内可导，那么在区间（a，b）内至少有一点ξ（a＜ξ＜b），使等式
f（b）-f（a）=f′（ξ）（b-a） （1）
成立.
定理的几何意义（见图3-2）：如果连续曲线y=f（x）除端点A和B外处处具有不垂直于x轴的切线，那么曲线上至少有一点C，使曲线在点C处的切线平行于弦AB.
从罗尔定理的几何意义可以看出（见图3-1），由于f（a）=f（b），弦AB是平行于x轴的，因此点C处的切线实际上也平行于弦AB.由此可见，罗尔定理是拉格朗日中值定理的特殊情况.
从拉格朗日中值定理与罗尔定理的关系，自然想到利用后者来证明但在拉格朗日中值定理中不一定具备f（a）=f（b）这个条件，为此我们设想来构造一个与f（x）有密切关系的函数φ（x）（称为辅助函数），使φ（x）满足条件φ（a）=φ（b）.然后对φ（x）应用罗尔定理，再把对φ（x）所得的结论转化到f（x）上，进而证得所要的结果.
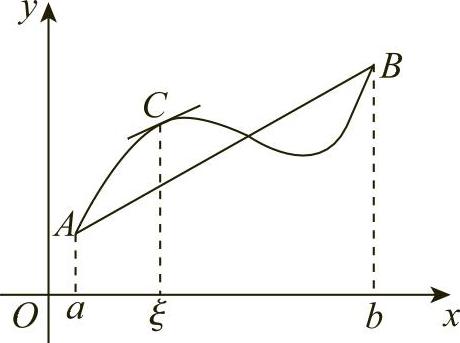
图3-2
下面我们从拉格朗日中值定理的代数结构来寻找辅助函数.由于式（1）可改写成
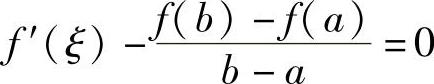
再分析等式左边的结构，因此可考虑函数一阶导数，并引入辅助函数：
容易验证函数φ（x）满足罗尔定理的条件：
φ（x）在闭区间[a，b]上连续，在开区间（a，b）上可导，且
根据罗尔定理可知，在区间（a，b）内至少有一点ξ，满足φ′（ξ）=0，即
由此得
也就是说 f（b）-f（a）=f′（ξ）（b-a）
显然，式（1）对于b＜a也成立.式（1）也叫作拉格朗日中值公式.
设x为区间[a，b]内一点，x+Δx为该区间内的另一点（Δx＞0或Δx＜0），则式（1）在区间[x，x+Δx]（当Δx＞0时）或在区间[x+Δx，x]（当Δx＜0时）上成为
f（x+Δx）-f（x）=f′（x+θΔx）Δx（0＜θ＜1） （2）
这里θ在0与1之间，所以x+θΔx在x与x+Δx之间.如果记f（x）为y，则式（2）又可写成 Δy=f′（x+θΔx）Δx（0＜θ＜1） （3）
我们知道，函数的微分dy=f′（x）Δx是函数的增量Δy的近似表达式.一般来说，以dy近似代替Δy时所产生的误差只有当Δx→0时才趋近于零，而式（3）则表示f′（x+θΔx）Δx在Δx为有限增量时Δy的准确表达式，因此这个定理也叫作有限增量定理.它在微分学中占有重要的地位，有时也叫作微分中值定理.它精确地表达了函数在一个区间上的增量与函数在这个区间内某点处的导数之间的关系.在某些问题中，当自变量x取得有限增量Δx而需要函数增量的准确表达式时，拉格朗日中值定理就显出了它的价值.(www.xing528.com)
作为拉格朗日中值定理的一个应用，下面我们来导出积分学中一个很有用的定理.
定理4 如果函数f（x）在区间I上的导数恒为零，那么f（x）在区间I上是一个常数.
证明 在区间I上任取两点x1，x2（x1＜x2），由拉格朗日中值定理可得
f（x2）-f（x1）=f′（ξ）（x2-x1）（x1＜ξ＜x2）
根据假定，f′（ξ）=0，所以f（x2）-f（x1）=0
即 f（x2）=f（x1）
因为x1，x2是I上任意两点，所以上面的等式表明：f（x）在I上的函数值总是相等的.也就是说，f（x）在区间I上是一个常数.
例2 证明：∀x1，x2∈R，恒有sinx1-sinx2≤x1-x2.
证明 设有函数y=sinx，x∈[x1，x2]，则y=sinx在区间[x1，x2]上连续且在区间（x1，x2）上可导，由拉格朗日中值定理可知，∃ξ∈（x1，x2），满足
所以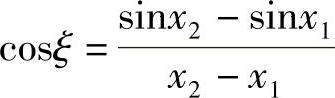
则
即 sinx2-sinx1≤x2-x1
例3 证明：当x＞0时，
.
证明 设有函数f（x）=ln（1+x）（x＞0），显然f（x）在区间[0，x]上满足拉格朗日中值定理的条件，因此有
f（x）-f（0）=f′（ξ）x（0＜ξ＜x）
由于f（0）=0，
，因此上式即为
又0＜ξ＜x，1＜ξ+1＜1+x，所以
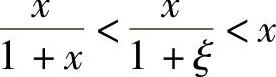
即
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
