高等数学.上册：微分的概念与引例

1.引例

一个正方形的边长为x，则其面积为

A=x²

若边长从x增加到x+Δx，则其面积的增量为

ΔA=A（x+Δx）-A（x）=（x+Δx）²-x²

=2x·Δx+（Δx）²

由上式及图26不难看出，其面积的增量由两部分组成：第一部分为2x·Δx，且是Δx的线性函数；第二部分为（Δx）²，且是Δx的高阶无穷小量.当Δx很小时，ΔA可以用第一部分，即2x·Δx来近似代替，其误差为Δx的高阶无穷小量，即

ΔA≈2x·Δx

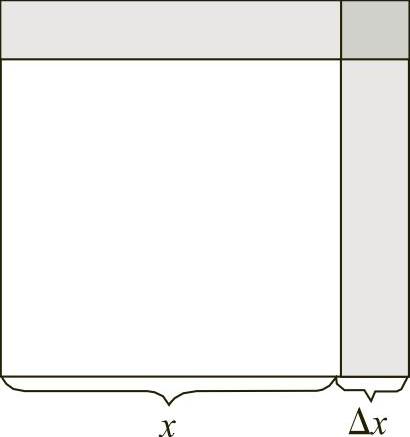
图2-6

2.微分的定义

定义 设函数y=f（x）在x的某邻域内有定义，x及x+Δx是该邻域内的点，若

Δy=f（x+Δx）-f（x）=A·Δx+ο（Δx）

其中A是不依赖于Δx的常数，ο（Δx）是比Δx高阶的无穷小，则称y=f（x）在点x处可微，A·Δx称为y=f（x）在点x处的微分，记作

dy=A·Δx

3.可微与可导的关系

定理 函数y=f（x）在点x处可微当且仅当函数y=f（x）在点x处可导.

证明 设函数y=f（x）在点x处可微，依定义则有

Δy=f（x+Δx）-f（x）=A·Δx+ο（Δx）

其中ο（Δx）是关于Δx的高阶无穷小，从而(www.xing528.com)

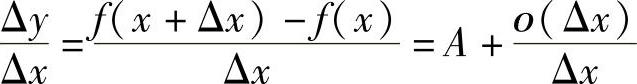
于是

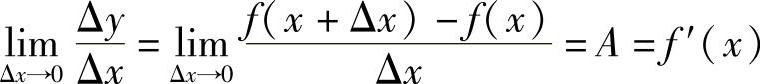
由此可知，函数y=f（x）在点x处可导，且f′（x）=A.

反之，设函数y=f（x）在点x处可导，则有

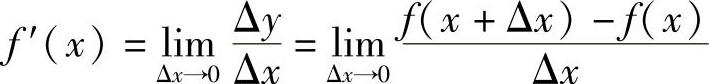
由极限与无穷小之间的关系可得

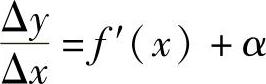
其中α是关于Δx的高阶无穷小，从而

Δy=f′（x）·Δx+α·Δx

由于f′（x）不依赖于Δx，而α·Δx=ο（Δx），所以函数y=f（x）在点x处可微.

由上述定理不但可以看到可微与可导是等价的，而且还能得到微分与导数的关系式.通常称自变量x的增量Δx为自变量的微分，记为dx，即

dx=Δx

那么函数y=f（x）的微分又可记为

dy=f′（x）dx

即函数的微分等于导数与自变量的微分的乘积，而上式又可改写为

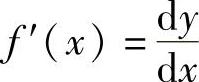
即函数的导数等于函数微分与自变量微分的商，因此导数又称为“微商”.

以前，我们将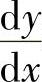看作运算记号的整体，在有了微分概念以后，可将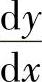看作是一个分式了.