简化为：复合函数求导法则及推广

定理2 设y=f[φ（x）]是由y=f（u），u=φ（x）复合而成，若u=φ（x）在点x处可导，而y=f（u）在点u处可导，则y=f[φ（x）]在点x处可导，且

证明 由于y=f（u）在点u处可导，因此

则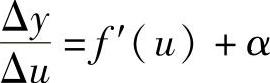

其中α是Δu→0的无穷小.所以

Δy=f′（u）Δu+αΔu

即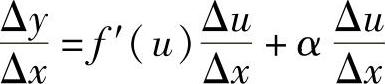

于是

注意：（1）此求导法则称为链式法则，并可推广到由多个函数构成的复合函数的情形.如y=f（u），u=φ（v），v=ω（x），则y=f[φ（ω（x））]可导，且

（2）正确运用此法则的关键在于弄清复合函数的函数关系.

例8 求y=（1+2x）⁸（n∈N）的导数y′.

解y=（1+2x）⁸可看作由y=u⁸，u=1+2x复合而成，因此

例9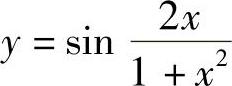，求.

解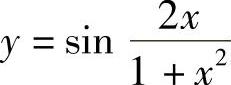可看作由y=sinu，复合而成，又因为

所以(www.xing528.com)

从以上例子可以看出，应用复合函数求导法则时，首先要分析所给函数可看作由哪些函数复合而成，或者说，所给函数能分解成哪些函数.如果所给函数能分解成比较简单的函数，而这些简单函数的导数我们已经会求，那么应用复合函数求导法则就可以求所给函数的导数了.

对复合函数的分解比较熟练后，就不必再写中间变量，而可以采用下列例题的方式来计算.

例10y=lntanx，求.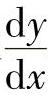

解

例11.

解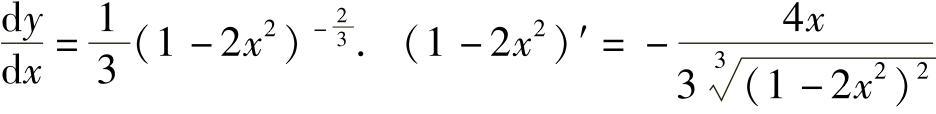

例12y=lncose^x，求.

解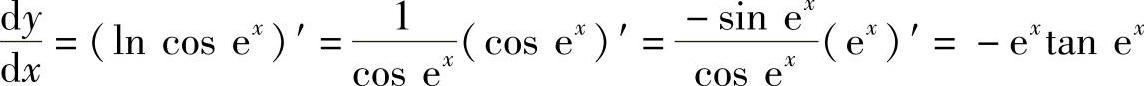

例13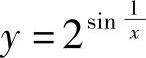，求.

解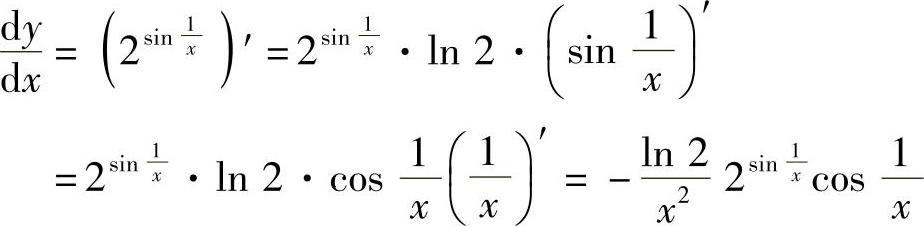

例14 设y=f（x）可导，求[f（lnx）]′，｛f[（x+a）n]｝′.

解

｛f[（x+a）n]｝′=f′[（x+a）n][（x+a）n]′=n（x+a）n-1f′[（x+a）n]