例5 由电学知识知道:对电容器充电过程中,电容器两端的电压uC随时间t增大的规律为
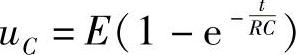
如图1-27所示,那么对电容器无限充电过程中,电压uC可以达到什么程度?
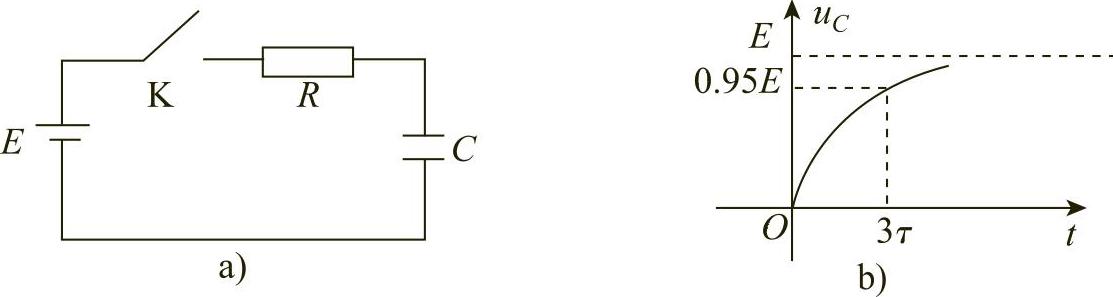
图1-27
由于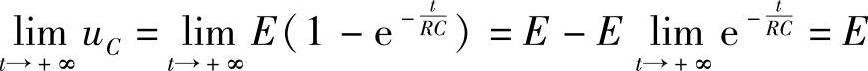 ,所以当充电时间无限增加时,电压uC与E无限接近.在电学中,称τ=RC为时间常数.当t=3τ=3RC时,有
,所以当充电时间无限增加时,电压uC与E无限接近.在电学中,称τ=RC为时间常数.当t=3τ=3RC时,有
uC=E(1-e-3)≈0.95E
当t>3τ时,uC增加速度变慢,于是通常将3τ作为电容器的充电时间.并且还能看出当τ越大,充电时间会越大.
例6 已知一个4Ω的电阻与一个可变电阻R并联,如图1-28所示,求当可变电阻R的支路突然断路时电路的总电阻.
解 由于4Ω的电阻与电阻R并联,那么总电阻为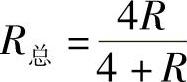 .
.
当可变电阻R的支路突然断路时,可以认为R→+∞,从而此时的总电阻为极限
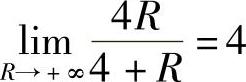
所以当可变电阻R的支路突然断路时电路的总电阻为4Ω.
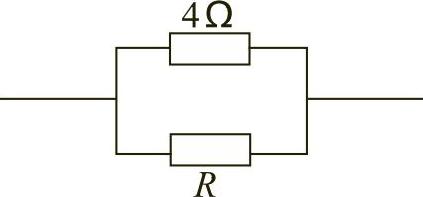
图1-28
例7 已知生产x对汽车挡泥板的成本函数为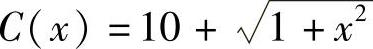 ,销售x对的收入函数R(x)=5x.
,销售x对的收入函数R(x)=5x.
(1)若出售x+1对比出售x对所产生的利润增长额为
I(x)=[R(x+1)-C(x+1)]-[R(x)-C(x)]
当生产稳定、产量很大时,这个增长额为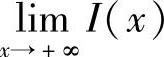 ,试求这个极限.
,试求这个极限.
(2)生产x对挡泥板时,每对的平均成本为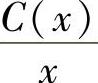 ,当产量很大时,每对的成本大致为
,当产量很大时,每对的成本大致为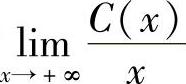 ,试求这个极限.(https://www.xing528.com)
,试求这个极限.(https://www.xing528.com)
解 (1)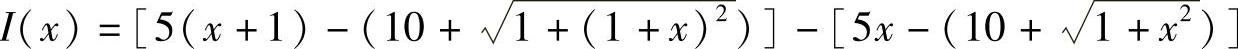
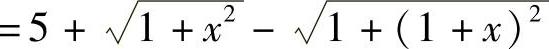
所以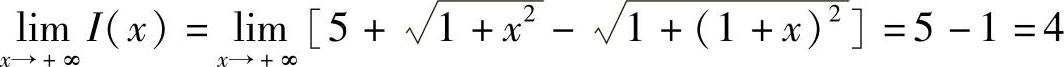
(2)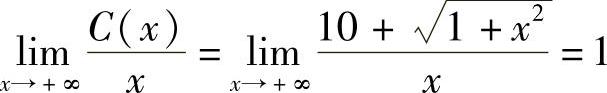
例8 连续复利问题.设有一笔贷款A0(称本金),年利率为r,则一年末结算时,其本利之和为
A1=A0+rA0=A0(1+r)
二年后的本利和为
A2=A1(1+r)=A0(1+r)2
k年后的本利和为
Ak=A0(1+r)k
如果一年分两期计息,每期利率为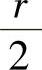 ,且前一期的本利之和作为后一期的本金,则一年末的本利之和为
,且前一期的本利之和作为后一期的本金,则一年末的本利之和为
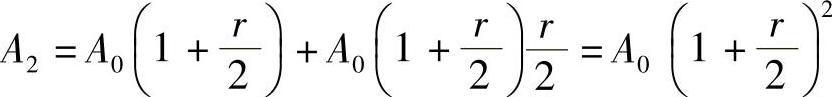
如果一年分n期计息,每期利率按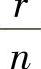 计算,且前一期本利之和为后一期的本金,则一年末的本利之和为
计算,且前一期本利之和为后一期的本金,则一年末的本利之和为
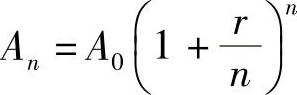
于是t年末共计算利nt次,其本利和为
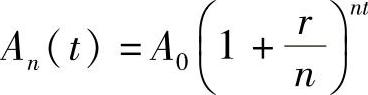
令n→∞,则表示利息随时计入本金(即连续复利).这样t年末的本利之和为
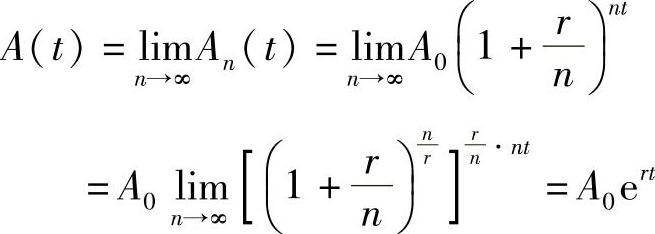
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




