【摘要】:前面我们已证明了三角函数及反三角函数在定义域内是连续的.在中学数学中已得出指数函数y=ax(a>0且a≠1)对于一切实数x都有定义,且在区间(-∞,+∞)内单调连续.由指数函数的单调性及连续性可得,对数函数y=logax(a>0且a≠0)在区间(0,+∞)内单调连续.幂函数y=xμ的定义域随μ的值而定,但无论μ为何值,函数在区间(0,+∞)内总有定义.根据复合函数的连续性,可以证明在区间(0,+∞
前面我们已证明了三角函数及反三角函数在定义域内是连续的.
在中学数学中已得出指数函数y=ax(a>0且a≠1)对于一切实数x都有定义,且在区间(-∞,+∞)内单调连续.
由指数函数的单调性及连续性可得,对数函数y=logax(a>0且a≠0)在区间(0,+∞)内单调连续.
幂函数y=xμ的定义域随μ的值而定,但无论μ为何值,函数在区间(0,+∞)内总有定义.根据复合函数的连续性,可以证明 在区间(0,+∞)内连续,即幂函数在定义域内是连续的.
在区间(0,+∞)内连续,即幂函数在定义域内是连续的.
综上可得,基本初等函数在它们的定义域内都是连续的.根据初等函数的定义及前面的论述可知:一切初等函数在定义域内都是连续的.
根据连续函数的定义,如果f(x)在点x0处连续,那么求f(x)在x→x0的极限时,只需要求出其函数值就行了,即当点x0在初等函数f(x)的定义域内时,有
例3 求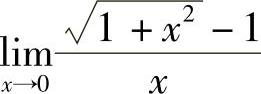 .解
.解 .
.
例4 求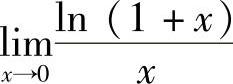 .解
.解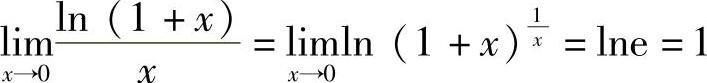 .
.
例5 求 .(https://www.xing528.com)
.(https://www.xing528.com)
解 令ax-1=t,则x=loga(1+t),且当x→0,t→0,于是
例6 求 .
.
解 .
.
一般地,形如u(x)v(x)(u(x)>0且u(x)≠1)的函数,既不是指数函数也不是幂函数(通常称为幂指函数),如果
limu(x)=a>0,limv(x)=b
那么
limu(x)v(x)=ab
这里的lim表示在同一极限过程中的极限.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




