反函数与复合函数的连续性

定理2 如果函数y=f（x）在区间I_x上单调增加（或单调减少）且连续，那么它的反函数x=f^-1（y）在对应区间I_y=｛y∣y=f（x），x∈I_x｝上单调增加（或单调减少）且连续.

证明从略.

可以证明，y=sinx在区间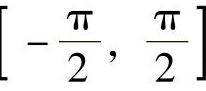上单调增加且连续，所以它的反函数y=arcsinx在区间[-1，1]上也是单调增加且连续的.另外，反三角函数y=arccosx，y=arctanx，y=arccotx在它们的定义域内都是连续的.

定理3 假设函数y=f[g（x）]由函数y=f（u）与u=g（x）复合而成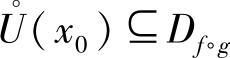，.若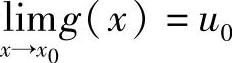，而函数y=f（u）在u=u₀处连续，则

证明参见第五节定理5.

说明 （1）上式可表示为，即求复合函数f[g（x）]的极限时，函数符号f与极限符号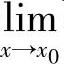可以换序.

（2）定理3中的x→x₀换为x→∞可得类似的定理.

例1 求.(www.xing528.com)

解 .

定理4 函数y=f[g（x）]由函数y=f（u）与函数u=g（x）复合而成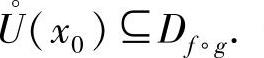，若函数u=g（x）在x=x₀处连续，且g（x₀）=u₀，而函数y=f（u）在u=u₀处连续，则复合函数y=f[g（x）]在x=x₀处也连续.

证明 只要在定理3中令u₀=g（x₀）就表示g（x）在点x₀处也连续，于是

即f[g（x）]在点x₀处连续.

例2 讨论函数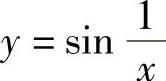的连续性.

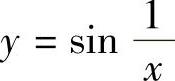解 因为函数由y=sinu及复合而成.sinu当-∞＜u＜+∞时连续，当-∞＜x＜0和0＜x＜+∞时连续，根据定理4，函数在区间（-∞，0）和（0，+∞）内连续.