无穷小的比较-高等数学.上册

由第五节知道，两个无穷小的和、差、积仍为无穷小，但两个无穷小的商却出现不同的情况.例如，当x→0时，x，x²，sinx都是无穷小，但

这反映了不同的无穷小趋于零的“快慢”是不一样的.就上面的例子而言，在x→0的过程中，x²→0比x→0“快些”，x→0比x²→0“慢些”，sinx→0与x→0的“快慢相仿”，由此有下面的定义.

定义 设limf（x）=0，limg（x）=0且g（x）≠0，

如果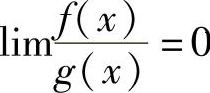，就说f（x）是比g（x）高阶的无穷小，记为f（x）=o[g（x）]；

如果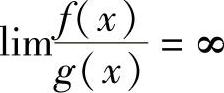，就说f（x）是比g（x）低阶的无穷小；

如果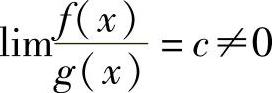，就说f（x）与g（x）是同阶无穷小；

如果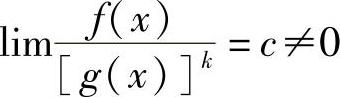，就说f（x）是关于g（x）的k阶无穷小；

如果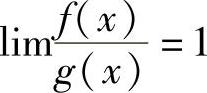，就说f（x）与g（x）是等价无穷小，记为f（x）～g（x）.

显然等价无穷小是同阶无穷小在c=1时的特殊情形.

下面举一些例子说明：

因为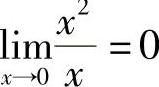，所以当x→0时，x²是比x高阶的无穷小，即x²=o（x）；

因为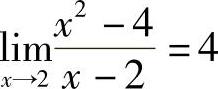，所以当x→2时，x²-4与x-2是同阶无穷小；

因为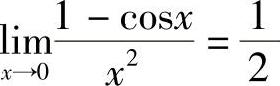，所以当x→0时，1-cosx是关于x的二阶无穷小；

因为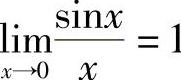，所以当x→0时，sinx与x是等价无穷小.

下面介绍几个常用的等价无穷小.

例1 证明：当x→0时，(www.xing528.com)

证明 因为

所以

例2 证明：当x→0时，.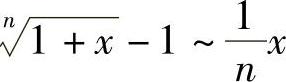

证明 因为

所以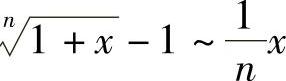

关于等价无穷小有下面的定理.

定理 设α～α′，β～β′，α≠0，且l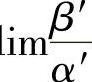存在，则

证明 .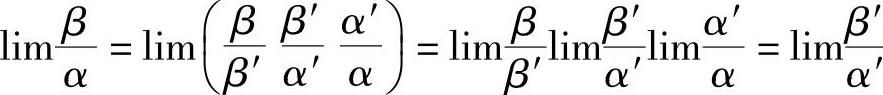

上述定理表明，求两个无穷小之比的极限时，分子、分母都可用等价无穷小来代替，这样可以简化极限的计算.

例3 求.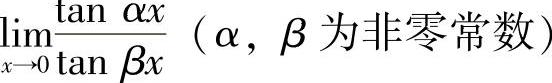

解 当x→0时，tanαx～αx，tanβx～βx，所以

例4 求.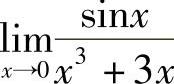

解 当x→0时，sinx～x，而无穷小x³+3x与它自身是等价的，所以

例5 求.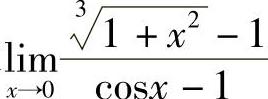

解 当x→0时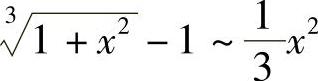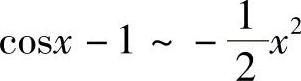，，，所以