本节将介绍判定极限存在的两个准则以及作为准则应用例子的两个重要极限:

准则1 如果数列{xn},{yn},{zn}满足下列条件,
(1)yn≤xn≤zn,
(2) ,
, ,
,
那么数列{xn}的极限存在,且 .
.
证明 因为 ,则∀ε>0,∃N1,当n>N1时,有
,则∀ε>0,∃N1,当n>N1时,有
a-ε<yn<a+ε (1)
又 ,则∀ε>0,∃N2,当n>N2时,有
,则∀ε>0,∃N2,当n>N2时,有
a-ε<zn<a+ε (2)
取N=max{N1,N2},当n>N时,式(1)和式(2)同时成立,则
a-ε<yn≤xn≤zn<a+ε
即 xn-a<ε
成立,这就证明了

上述数列极限存在准则可以推广到函数的极限.
推论 如果
(1)当 (或x>M)时,
(或x>M)时,
g(x)≤f(x)≤h(x),
(2) ,
, ,那么
,那么 存在,且
存在,且 .
.
准则1及其推论称为夹逼准则.
作为准则1的应用,我们来证明一个重要极限:

证明 如图1-13所示,作单位圆.设圆心角


图1-13
点A处的切线与OP的延长线相交于T,又因为PQ⊥OA,则

因为 ,所以
,所以

即  或
或
因为用-x代替x时,cosx与 的符号都不变,所以上面式子对于开区间
的符号都不变,所以上面式子对于开区间 内一切x也成立,而且
内一切x也成立,而且 .故当
.故当 时,
时,

即
当x→0时, ,所以
,所以
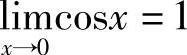
由推论,即得
 (https://www.xing528.com)
(https://www.xing528.com)
例1 求 .
.
解
例2 求 .
.
解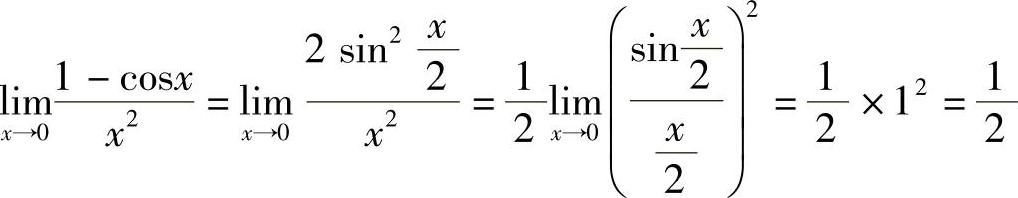
例3 求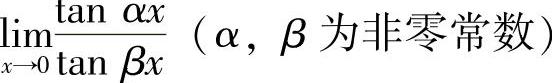 .
.
解
例4 求 .
.
解 令arcsinx=t,则x=sint,当x→0,t→0,于是有

准则2 单调有界数列必有极限.
如果数列{xn}满足条件
x1≤x2≤…≤xn≤xn+1≤…
则称数列{xn}是单调增加的;如果数列{xn}满足条件
x1≥x2≥…≥xn≥xn+1≥…
则称数列是单调减少的.单调增加和单调减少统称为单调.
对于准则2,我们不进行证明.作为应用我们讨论另一个重要极限:
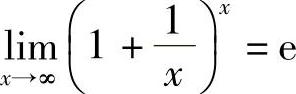
下面考虑x取正整数n而且趋于+∞的情形.
设 ,我们来证数列{xn}单调增加且有界.按二项式展开,则
,我们来证数列{xn}单调增加且有界.按二项式展开,则

容易得出

且0<xn<xn+1,说明{xn}单调增加且有界.
根据极限存在准则2,这个数列的极限存在,通常用字母e来表示,即
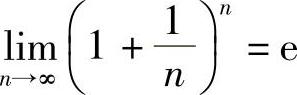
可以证明,当x取实数而趋于+∞或-∞时,函数 的极限存在且等于e,因此
的极限存在且等于e,因此

这个数e是无理数,它的值是
e=2.718281828459045…
利用极限运算法则有

实际上,在上式中令 ,当x→0时,z→∞.
,当x→0时,z→∞.
例5 求 .
.
解 令t=-x,则x→∞时,t→∞,于是有
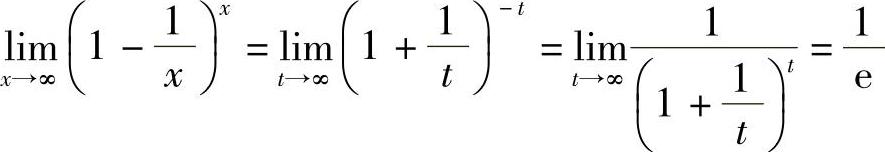
推论 f(x)在点x0的某个左邻域内单调有界,则f(x)在x0的左极限f(x0-)必定存在.
例6 求 .
.
解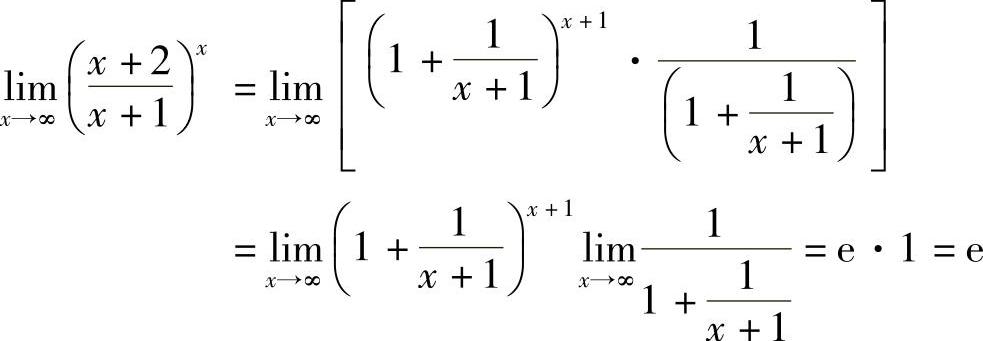
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




