数列极限运算法则简明解析

本节主要讨论极限运算法则，其中包括四则运算法则、复合函数的极限运算法则.

在下面的讨论中，只针对x→x₀及x→∞的情形，为方便起见，简记为“lim”.而在证明中，只证当x→x₀时的情形，x→∞的情形留给学生思考.

定理1 有限个无穷小的和仍为无穷小.

证明 实际上只需要证明两个无穷小的和仍为无穷小即可.

设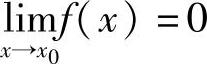，则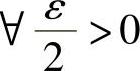，∃δ₁＞0，当0＜∣x-x₀∣＜δ₁时，有

又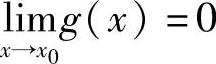，则，∃δ₂＞0，当0＜∣x-x₀∣＜δ₂时，有

记φ（x）=f（x）+g（x），对相同的ε，取δ=min｛δ₁，δ₂｝，则当0＜∣x-x₀∣＜δ时，有

同理可证，有限个无穷小的和仍为无穷小.

定理2 有界函数与无穷小量的积仍为无穷小.

证明 设函数f（x）在x₀的某个去心邻域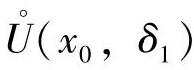内有界，即∃M＞0，使

f（x）＜M

对一切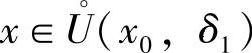成立.又设α（x）是当x→x₀时的无穷小，即∀ε＞0，对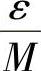，∃δ₂＞0，

当0＜∣x-x₀∣＜δ₂时，有

取δ=min｛δ₁，δ₂｝，则当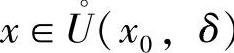时，有

同时成立，从而

推论1 常数与无穷小的乘积仍为无穷小.

推论2 有限个无穷小的乘积仍是无穷小.

定理3 如果limf（x）=A，limg（x）=B，那么

（1）lim[f（x）±g（x）]=limf（x）±limg（x）=A±B；

（2）lim[f（x）g（x）]=limf（x）limg（x）=AB；

（3）若B≠0，则.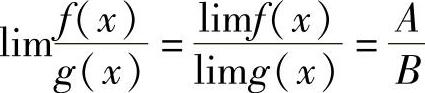

证明 先证（1）.

因为limf（x）=A，limg（x）=B，则有

f（x）=A+α（x），g（x）=B+β（x）

其中α（x），β（x）均为无穷小.于是

f（x）±g（x）=A±B+（α（x）±β（x））

所以

lim[f（x）±g（x）]=A±B=limf（x）±limg（x）

（2）（3）留给学生证明.

定理3中的（1）（2）可以推广到有限个函数的情形.

推论1 如果limf（x）存在，C为常数，则(www.xing528.com)

limCf（x）=Climf（x）

也就是说，常数因子可以提到极限符号外面，这是因为limC=C.

推论2 如果limf（x）存在，而n∈N^∗，则

lim[f（x）]ⁿ=[limf（x）]ⁿ

这是因为

lim[f（x）]ⁿ=lim[f（x）·f（x）·…·f（x）]=limf（x）·limf（x）·…·limf（x）=[limf（x）]ⁿ

关于数列，也有类似的四则运算法则.

定理4 设数列{x_n}和{y_n}，如果limx_n=A，limy_n=B，那么

（1）lim（x_n±y_n）=A±B；

（2）limx_ny_n=AB；

（3）当y_n≠0（n=1，2，…）且B≠0时，.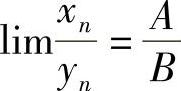

证明从略.

例1 求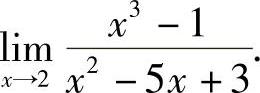

解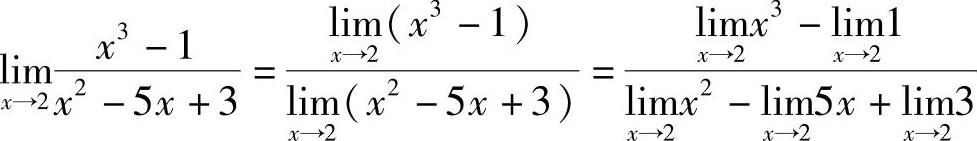

例2 求.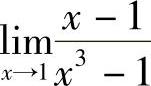

解 因为x→1，但x≠1，故可通过分解因式约去趋于零的因式，所以

例3 求.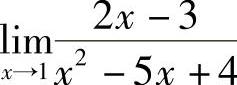

解 因为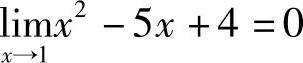，而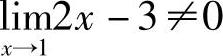，因此不能用极限法则，但

故

例4 求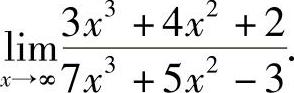

解.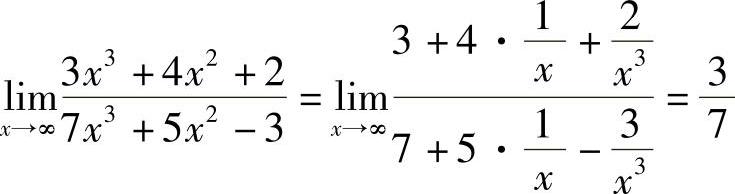

例5 求.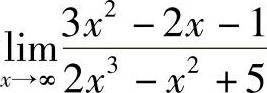

解.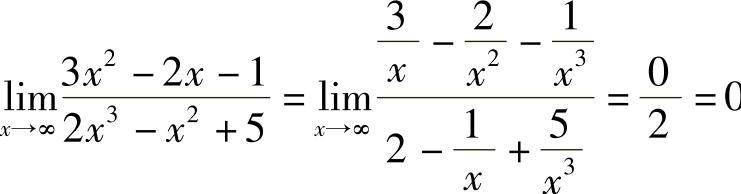

例6 求.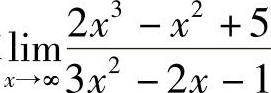

解 因为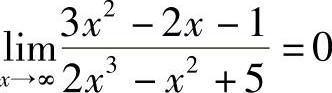，所以

由例4、例5、例6可以看出，当a₀≠0，b₀≠0，m，n为非负整数时，有

例7 求.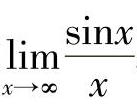

解 当x→∞时，分子、分母的极限均不存在，故不能用商的极限运算法则，但可将视为sinx与的乘积.由于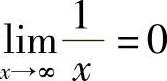，而sinx≤1，根据定理2有

定理5 （复合函数的极限运算法则）设函数y=f[g（x）]是由函数y=f（u）与函数u=g（x）复合而成的，而且f[g（x）]满足在点x₀的某个去心邻域内，若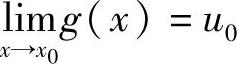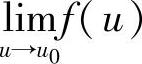，=A，且存在δ₀＞0，当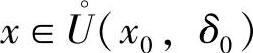时，有g（x）≠u₀，则