无穷大的定义及特性-高等数学.上册

定义2 设函数f（x）在x₀的某一去心邻域内（或∣x∣大于某一正数时）有定义，如果对于任意给定的正数M（无论它多么大），总存在正数δ（或正数X），使得对于满足不等式0＜∣x-x₀∣＜δ（或∣x∣＞X）的一切x，其对应的函数值f（x）总满足不等式

∣f（x）∣＞M

则称函数f（x）为当x→x₀（或x→∞）时的无穷大量，简称无穷大.

当x→x₀（或x→∞）时的无穷大函数f（x），按函数极限定义来讲，其极限是不存在的，但为了便于叙述函数的极限概念，我们也说“函数的极限是无穷大”，记作

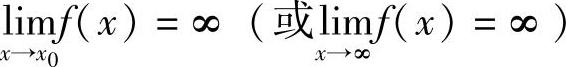
注意：无穷大∞不是数，不可与很大的数混为一谈.

下面是对几种情形的叙述：

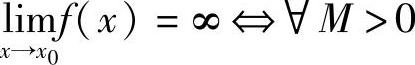，∃δ＞0，当0＜∣x-x₀∣＜δ时，有∣f（x）∣＞M.

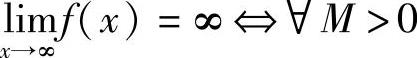，∃X＞0，当∣x∣＞X时，有∣f（x）∣＞M.

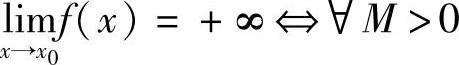，∃δ＞0，当0＜∣x-x₀∣＜δ时，有f（x）＞M.

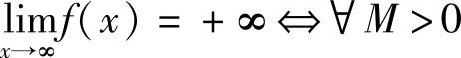，∃X＞0，当∣x∣＞X时，有f（x）＞M.

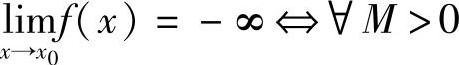，∃δ＞0，当0＜∣x-x₀∣＜δ时，有f（x）＜-M.

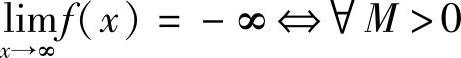，∃X＞0，当∣x∣＞X时，有f（x）＜-M.

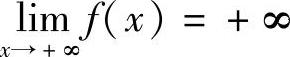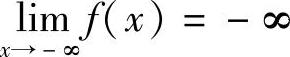，又该怎样表述，请学生自己考虑.

例2 证明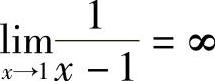：（见图1-12）.(www.xing528.com)

证明 ∀M＞0，要使

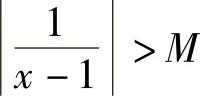
只需要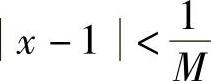

取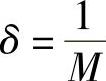，则当0＜x-1＜δ时，有

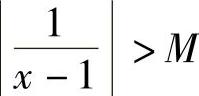
所以

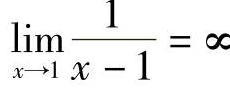
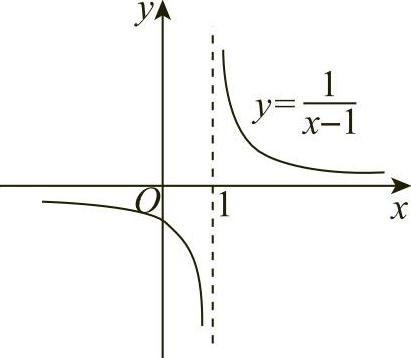
图1-12

直线x=1是函数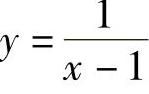的铅直渐近线.

一般地，如果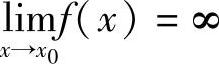，则直线x=x₀是函数y=f（x）的铅直渐近线.

定理2 在自变量的同一变化过程中，如果f（x）为无穷大，则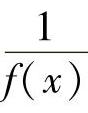为无穷小；反之，

如果f（x）为无穷小，且f（x）≠0，则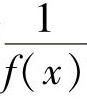为无穷大.

证明留给学生.