【摘要】：定义1 设函数f（x）在x0的某一去心领域内（或∣x∣大于某一正数时）有定义，如果对于任意给定的正数ε（无论它多么小），总存在正数δ（或正数X），使得对于满足不等式0＜∣x-x0∣＜δ（或∣x∣＞X）的一切x，其对应的函数值f（x）总满足不等式∣f（x）∣＜ε则称函数f（x）为当xx0（或x∞）时的无穷小量，简称无穷小，记作例1 证明：.证明 ε＞0，要使只需要取，则当x＞X时，有所以注意：不要把
定义1 设函数f（x）在x0的某一去心领域内（或∣x∣大于某一正数时）有定义，如果对于任意给定的正数ε（无论它多么小），总存在正数δ（或正数X），使得对于满足不等式0＜∣x-x0∣＜δ（或∣x∣＞X）的一切x，其对应的函数值f（x）总满足不等式
∣f（x）∣＜ε
则称函数f（x）为当x➝x0（或x➝∞）时的无穷小量，简称无穷小，记作
例1 证明：
.
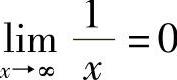证明 ∀ε＞0，要使
只需要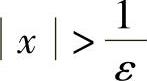
取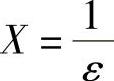
，则当x＞X时，有
所以
注意：不要把无穷小与很小的数混为一谈.
无穷小与函数极限之间的关系.
定理1 在自变量的同一变化过程x→x0（或x→∞）中，函数f（x）具有极限A的充分必要条件是f（x）=A+α（x），其中α（x）是无穷小.
证明 必要性：(www.xing528.com)
设
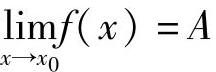，则∀ε＞0，∃δ＞0，当0＜∣x-x0∣＜δ时，有
∣f（x）-A∣＜ε
令α（x）=f（x）-A，则α（x）是当x→x0时的无穷小，且
f（x）=A+α（x）
充分性：
设f（x）=A+α（x），其中A是常数，α（x）是当x→x0时的无穷小，于是
∣f（x）-A∣=∣α（x）∣
因为α是当x→x0时的无穷小，所以∀ε＞0，∃δ＞0，当0＜∣x-x0∣＜δ时，有
∣α（x）∣＜ε
即 ∣f（x）-A∣＜ε
类似地可以证明当x→∞时的情形.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
