【摘要】:由于函数极限的定义按自变量x的不同的变化过程有各种形式,所以下面仅以“”这种形式为代表给出函数极限的一些性质.至于其他形式的函数的极限性质,只需要进行相应的修改即可证明.定理1 (函数极限的唯一性)如果存在,那么极限唯一.定理2 (函数极限的局部有界性)如果,那么存在常数M>0和δ>0,使得当0<∣x-x0∣<δ时,有∣f(x)∣<M证明 因为,所以取ε=1,则δ,当0<∣x-x0∣<δ时,有∣f
由于函数极限的定义按自变量x的不同的变化过程有各种形式,所以下面仅以“ ”这种形式为代表给出函数极限的一些性质.至于其他形式的函数的极限性质,只需要进行相应的修改即可证明.
”这种形式为代表给出函数极限的一些性质.至于其他形式的函数的极限性质,只需要进行相应的修改即可证明.
定理1 (函数极限的唯一性)如果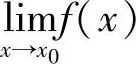 存在,那么极限唯一.
存在,那么极限唯一.
定理2 (函数极限的局部有界性)如果 ,那么存在常数M>0和δ>0,使得当0<∣x-x0∣<δ时,有
,那么存在常数M>0和δ>0,使得当0<∣x-x0∣<δ时,有
∣f(x)∣<M
证明 因为 ,所以取ε=1,则∃δ,当0<∣x-x0∣<δ时,有
,所以取ε=1,则∃δ,当0<∣x-x0∣<δ时,有
∣f(x)-A∣<1⇒∣f(x)∣≤∣f(x)-A∣+∣A∣<∣A∣+1
取M=∣A∣+1,即可得证.
定理3 (函数极限的局部保号性)如果 ,而且A>0(或A<0),那么存在常数δ>0,使得当0<∣x-x0∣<δ时,有
,而且A>0(或A<0),那么存在常数δ>0,使得当0<∣x-x0∣<δ时,有
f(x)>0(或f(x)<0)
证明 就A>0的情形证明.
因为 ,所以取
,所以取 ,∃δ>0,当0<∣x-x0∣<δ时,有
,∃δ>0,当0<∣x-x0∣<δ时,有
类似可以证明A<0的情况.(https://www.xing528.com)
推论1 如果 ,那么存在x0的某一去心邻域
,那么存在x0的某一去心邻域 ,当
,当 时,有
时,有
推论2 如果在x0的某一去心邻域内,f(x0)≥0(或f(x0)≤0),且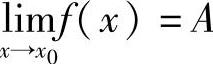 ,那么A≥0(或A≤0).
,那么A≥0(或A≤0).
定理4 (函数极限与数列极限之间的关系)如果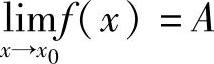 ,{xn}为函数f(x)的定义域内任一收敛于x0的数列,且满足xn≠x0(n∈N∗),那么相应的函数值数列{f(xn)}必收敛,且
,{xn}为函数f(x)的定义域内任一收敛于x0的数列,且满足xn≠x0(n∈N∗),那么相应的函数值数列{f(xn)}必收敛,且
证明 设 ,则∀ε>0,∃δ>0,当0<∣x-x0∣<δ时,有
,则∀ε>0,∃δ>0,当0<∣x-x0∣<δ时,有
∣f(x)-A∣<ε
又 ,则对δ>0,∃N,当n>N时,有
,则对δ>0,∃N,当n>N时,有
∣xn-x0∣<δ
由假设xn≠x0(n∈N∗),故当n>N时
0<∣xn-x0∣<δ
从而 ∣f(xn)-A∣<ε
所以
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




