定理1 (极限的唯一性)如果数列{xn}收敛,那么它的极限唯一.
证明 用反证法.
设同时有xn→a及xn→b且a<b,则取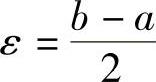 ,由
,由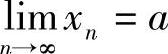 可知,
可知, ,∃N1,当n>N1时,有
,∃N1,当n>N1时,有
由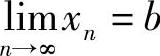 可知,
可知,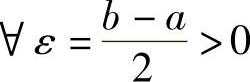 ,∃N2,当n>N2时,有
,∃N2,当n>N2时,有
取N=max{N1,N2},则当n>N时,式(1)和式(2)同时成立.但由式(1)有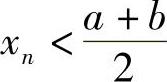 ,而由式(2)有
,而由式(2)有 ,这是不可能的.因此定理1成立.
,这是不可能的.因此定理1成立.
定理2 (收敛数列的有界性)如果数列{xn}收敛,那么数列{xn}一定有界.
证明 设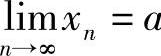 ,根据数列极限的定义,对于ε=1,∃N,当n>N时,不等式
,根据数列极限的定义,对于ε=1,∃N,当n>N时,不等式
∣xn-a∣<1
都成立.于是,当n>N时,有
∣xn∣=∣xn-a+a∣≤∣xn-a+a∣<1+a
取M=max{∣x1∣,∣x2∣,…,∣xN∣,1+∣a∣},那么对于数列{xn}中的一切xn,都满足
∣xn∣<M
这就证明了数列{xn}是有界的.
根据上述定理,如果{xn}无界,那么数列{xn}一定发散.但{xn}有界,却不能断定数列{xn}一定收敛.例如,数列
1,-1,1,…,(-1)n+1,…
有界,但该数列是发散的.因此数列有界是数列收敛的必要条件,但不是充分条件.
定理3 (收敛数列的保号性)如果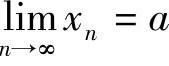 ,且a>0(或a<0),那么存在正整数N,当n>N时,都有
,且a>0(或a<0),那么存在正整数N,当n>N时,都有
xn>0(或xn<0)
证明 就a>0的情形证明.由数列极限的定义,对 ,∃N,当n>N时,有
,∃N,当n>N时,有
从而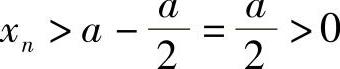 (https://www.xing528.com)
(https://www.xing528.com)
推论 如果数列{xn}从某一项起都有xn≥0(或xn≤0),且 ,那么
,那么
a≥0(或a≤0)
证明 设数列{xn}从第N1项起,即当n>N1时,有xn≥0.现用反证法证明.
若 ,则由定理3知,∃N2,当n>N2时,有
,则由定理3知,∃N2,当n>N2时,有
xn<0
取N=max{N1,N2},当n>N时,由假设有xn≥0.而由定理3,有xn<0,矛盾.故有
a≥0
数列{xn}从某一项起都有xn≤0的情形,可类似证明.
下面介绍子列的概念及关于收敛的数列与子列之间的关系定理.
在数列{xn}中任意抽取无限多项,并保持这些项在原数列{xn}中的先后次序,这样得到的一个数列称为原数列{xn}的子数列(或子列).
设在数列{xn}中,第一次抽取的记为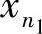 ,第二次在
,第二次在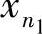 后抽取的记为
后抽取的记为 ,第三次在
,第三次在 后抽取的记为
后抽取的记为 ……这样无休止地抽取下去,得到一个数列
……这样无休止地抽取下去,得到一个数列
这个数列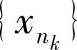 就是{xn}的一个子列.
就是{xn}的一个子列.
定理4 (收敛数列与其子列之间的关系)如果数列{xn}收敛于a,那么它的任何一个子列也收敛于a.
证明 设数列 是数列{xn}的任一子列.由于
是数列{xn}的任一子列.由于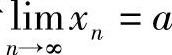 ,故∀ε>0,∃N,当n>N时,有
,故∀ε>0,∃N,当n>N时,有
∣xn-a∣<ε
成立.取K=N,则当k>K时,nk>nN≥N,于是
这就证明了
由定理4可知,如果数列{xn}有两个子列收敛于不同的极限,那么数列{xn}是发散的.例如,数列
1,-1,1,…,(-1)n+1,…的子列{x2k-1}收敛于1,而子列{x2k}收敛于-1,因此数列xn=(-1)n+1(n=1,2,…)是发散的,同时这个例子也说明了一个发散数列也可能有收敛的子数列.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




