掌握数列极限定义的方法

为了掌握变量的变化规律，有时不仅要考虑变量的变化过程，还要判断它的变化趋势.

例如，有一个变量，开始是1，然后变为，接着变为，然后是，，…，，…如此

一直无尽地变下去.虽然它是无尽的，但它的变化却有一个趋势，就是越来越接近于0.此时，我们就说这个变量的极限是0.高等数学中有很多重要的概念和方法都和极限有关，因此可以说极限是高等数学的一个重要的工具.在实际问题中，极限也占有重要地位，如求圆的面积和周长.我国古代数学家刘徽（公元3世纪）利用圆内接正多边形来推算圆面积的方法——割圆术，就是极限思想在几何上的应用.

设有一圆，首先构建内接正六边形，面积记为A₁；然后构建正十二边形，面积记为A2；再构建内接正二十四边形，面积记为A3……如此下去，每次边数增加一倍.一般地，把内接正6×2^n-1边形的面积记为A_n，这样就得到一系列内接正多边形的面积

A₁，A₂，A₃，…，A_n，…

它们构成一列有次序的数，当n越大时，内接正多边形的面积与圆的面积差别就越小，从而以A_n作为圆面积的近似值也越精确.但无论n取如何大，只要n取定了，A_n也只是多边形的面积，而不是圆的面积.如果n无限增大（记为n→∞，读作n趋于无穷大）时，内接正多边形的边数也无限增加，而在这个过程中，内接正多边形无限接近于圆.这个“无限接近”的过程就是一个极限过程.这时，A_n也无限接近某一确定的数值，这个确定的数值可理解为圆的面积.

我们首先说明数列的概念.如果按照某一法则，对于每一个n∈N^∗，都对应着一个确定的实数x_n.这些实数x_n按照下标n从小到大排列得到的一个序列

x₁，x₂，…，x_n，…

叫作数列，简记为｛x_n｝.

数列中的每一个数叫作数列的项，第n项叫作数列的一般项.

一些简单数列的例子：

，具体写出来就是：-1，，，，…

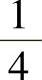，具体写出来就是：2，，，，…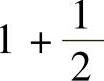

{n²}，具体写出来就是：1，4，9，16，…

｛1+（-1）n｝，具体写出来就是：0，2，0，2，…

数列｛x_n｝可看作自变量为正整数n的函数

x_n=f（n），n∈N^∗

当自变量n依次取1，2，3，…所有正整数时，对应的函数就排列成数列｛x_n｝.

现在我们关心的是：当n无限增大时（即n→∞时），对应的x_n=f（n）是否能无限接近于某个确定的数值.如果能，这个数值又等于什么？

从直观上容易看出，数列随着n的增大，越来越接近于1.但我们还是要进一步分析，如何用数学语言来表达.所谓数列越来越接近1，是指随着项数n的增加，越来越接近于1.换句话说，当n不断增大时，与1的差不断接近于0.

进一步说，随便给定一个无论多么小的正数ε，与1之差的绝对值总会小于这个ε，条件是n必须充分大.但究竟n要多大呢？只要按照下面的方法去做就可以了，即为了使得

解此不等式，可得

把上面的话连接起来就是：对于任意给定的ε＞0，只要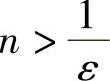，就能证明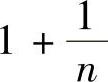与1之差的绝对值小于ε，这就意味着越来越接近1.把这句话抽象化，可得到数列极限的定义.

定义1　（数列极限的定义）设｛x_n｝为一数列，如果存在正常数a，对于任意给定的正数ε（无论它多么小），总存在一个正整数N，使得当n＞N时，不等式

∣x_n-a∣＜ε

都成立，我们就称常数a是数列｛x_n｝的极限，或称数列｛x_n｝收敛于a，记为

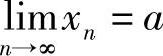
或x_n→a（n→∞）

如果不存在这样的常数a，就说数列｛x_n｝没有极限，或者说数列｛x_n｝是发散的，习惯上说不存在.

上面定义中的正数可以任意给定是很重要的.只有这样，不等式∣x_n-a∣＜ε才能表达出x_n与a无限接近的意思.此外，还应注意到，定义中的正整数N与任意给定的正数ε有关，它随着ε的给定而选定.

现在，我们给出数列极限的几何解释.在定义中不等式

∣x_n-a∣＜ε

就是 a-ε＜x_n＜a+ε(https://www.xing528.com)

它表示x_n在开区间（a-ε，a+ε）内.因此｛x_n｝以a为极限就是对于任意给定的一个开区间（a-ε，a+ε），第N项以后的一切数x_N+1，x_N+2，…全部落在这个区间内（见图1-9），而只有有限个（至多N个）在区间以外.

图1-9

为了表达方便，引入记号“∀”，它表示“对于任意给定的”或“对于每一个”；记号“∃”表示“存在”.于是“对于任意给定的ε＞0”可写成“∀ε＞0”；“存在正整数N”可写成“∃N”，而数列极限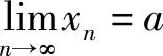的定义表达为

，N，当n＞N时，有∣x_n-a∣＜ε

数列极限的定义并没有直接提供求数列极限的方法，关于极限的求法后面再讲.现在举几个例子说明极限的概念以及如何用定义来考察数列的极限.

例1 证明数列

的极限是1.

证明 ∀ε＞0，要使

则有

取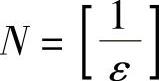，当n＞N时，有

总成立.故

例2 证明数列的极限是0.

证明 ∀ε＞0，要使

即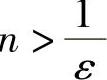

取，当n＞N时，有

总成立.故

例3 证明：.

证明当q=0时，显然有0.

当q≠0时， ∀ε＞0，要使

∣qⁿ-0∣=∣qⁿ∣＜ε

只要 nln∣q＜lnε

即

取，则当n＞N时，有

qⁿ＜ε

总成立.故0.