函数的概念定义、三要素及表示法

1.函数的概念

定义2 设有数集D⊆R，则映射f∶D→R为定义在D上的函数，记为

y=f（x），x∈D

其中x为自变量，y为因变量，D称为定义域，f（D）⊆R称为值域.

函数的三要素：定义域D、对应法则f、值域f（D）.

函数的表示法：表格法、图像法、解析法.

函数

的定义域D=（-∞，+∞），值域f（D）=[0，+∞），它的图像如图1-1所示.这个函数称为绝对值函数.

函数

的定义域D=（-∞，+∞），值域f（D）=｛-1，0，1｝，它的图像如图1-2所示.这个函数称为符号函数.对任意实数x，下列关系成立：

x=sgnx·∣x∣

图1-1

图1-2

设x为任意实数，不超过x的最大整数称为x的整数部分，记为[x].例如

把x看作变量，则函数

y=[x]

的定义域D=（-∞，+∞），值域f（D）=Z，它的图像如图1-3所示.其图像称为阶梯曲线，这个函数称为取整函数.

2.具有特殊性质的函数

（1）有界函数

设函数f（x）的定义域为D，如果存在一个数K，对于所有的x∈D，恒有

f（x）≤K（或f（x）≥K）

则称函数f（x）在D上是有上界（或下界）的.如果f（x）在D上既有上界又有下界，则称函数f（x）在D上有界，否则称它为在D上无界.

图1-3

（2）单调函数

设函数f（x）的定义域为D，区间I⊆D，如果对于任意的x₁，x₂∈I，满足

①当x₁＜x₂时，恒有

f（x₁）＜f（x₂）

则称f（x）在I上是单调增加的；

②当x₁＜x₂时，恒有

f（x₁）＞f（x₂）

则称f（x）在I上是单调减少的.

（3）奇偶函数

设函数f（x）的定义域D是关于原点对称的，如果对于任意x∈D，有

f（-x）=f（x）

恒成立，则称f（x）为偶函数；如果对于任意x∈D，有

f（-x）=-f（x）

恒成立，则称f（x）为奇函数.

（4）函数的周期性

设函数f（x）的定义域为D，如果存在一个l＞0，使对于任意x∈D，有x±l∈D，且

f（x+l）=f（x）

恒成立，则称f（x）为周期函数.l称为f（x）的周期，通常说函数的周期指的是最小正周期.

3.反函数

设函数f∶D→f（D）是单射，则它的逆映射f-1：f（D）→D称为函数f的反函数.一般地，函数y=f（x）的反函数记为

y=f^-1（x），x∈f（D）

4.复合函数

设函数y=f（u）的定义域为D₁，函数u=g（x）在D上有定义，且g（D）⊆D₁，则由下式确定的函数

y=f[g（x）]，x∈D

称为由函数u=g（x）和函数y=f（u）构成的复合函数.它的定义域为D，变量u称为中间变量.

5 . 函数的运算

假设函数f（x），g（x）的定义域分别为D₁，D₂，D=D₁∩D₂≠∅，则可以定义这两个函数的运算：

和、差的运算f±g：（f±g）（x）=f（x）±g（x），x∈D；

积的运算f·g：（f·g）（x）=f（x）g（x），x∈D；(www.xing528.com)

商的运算：，x∈D＼{x∣g（x）=0}.

6.初等函数

（1）基本初等函数

幂函数：y=x^α（α∈R，常数）.

指数函数：y=a^x（a＞0且a≠1）.

对数函数：y=log_ax（a＞0且a≠1）.特别地，当a=10时，记为y=lgx；当a=e时，记为y=lnx.

三角函数：y=sinx，y=cosx，y=tanx，y=cotx等.

反三角函数：y=arcsinx，y=arccosx，y=arctanx，y=arccotx等.

（2）初等函数

常数和基本初等函数经过有限次的四则运算和有限次的复合构成，并可以用一个式子表示的函数，称为初等函数.

（3）双曲函数

双曲正弦函数：；

双曲余弦函数：；

双曲正切函数：.

显然，双曲正弦函数的定义域为（-∞，+∞），它是奇函数，在定义域内它是单调增加的，它的图像在第一象限内随着x的增大接近于曲线，如图1-4所示.

双曲余弦函数的定义域为（-∞，+∞）.它是偶函数，其图像经过点（0，1），且关于y轴对称.在区间（-∞，0）内它是单调减少的，在区间（0，+∞）内它是单调增加的.它的图像随着x的增大，在第一象限内接近于曲线，而在第二象限内接近于曲线，如图1-4所示，ch0=1是这个函数的最小值.

双曲正切函数的定义域为（-∞，+∞）.它是奇函数，其图像通过原点，且关于原点对称.在区间（-∞，+∞）内它是单调增加的，其图像在水平直线y=1及y=-1之间，且当x很大时，在第一象限内接近于直线y=1，在第三象限内接近于直线y=-1，如图1-5所示.

图1-4

图1-5

根据双曲函数的定义，有下列公式：

sh（x+y）=shxchy+chxshy；

sh（x-y）=shxchy-chxshy；

ch（x+y）=chxchy+shxshy；

ch（x-y）=chxchy-shxshy；

ch²x-sh²x=1；

sh2x=2shxchx；

ch2x=ch²x+sh²x.

以上公式与三角函数的有关公式类似，把它们进行对比记忆.

反双曲函数，我们进行以下讨论.

反双曲正弦函数：y=arshx；

反双曲余弦函数：y=archx；

反双曲正切函数：y=arthx.

因为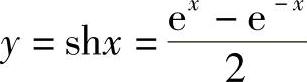

则e^2x-2ye^x-1=0

所以

又因为e^x＞0，所以

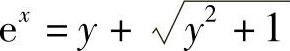
则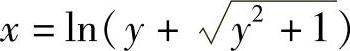

故得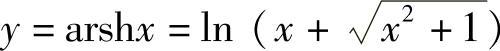

显然y=arshx的定义域为（-∞，+∞），它是奇函数，在区间（-∞，+∞）内是单调增加的.由y=shx可画y=arshx的图像，如图1-6所示.

下面讨论双曲余弦函数y=chx（x≥0）的反函数.由chx=y，有

由此得

故有

所以

其定义域为[1，+∞），在区间[1，+∞）上是单调增函数，如图1-7所示.

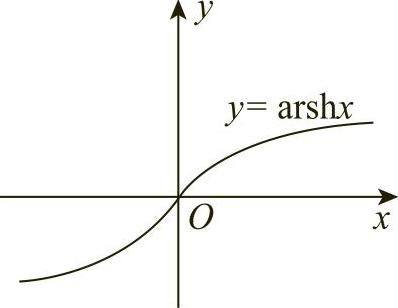
图1-6

图1-7

同理可得

它的定义域为（-1，1），在区间（-1，1）内是单调增函数，且是奇函数，其图像关于原点对称，如图1-8所示.

图1-8