【摘要】:1.映射概念定义1 设X,Y是两个非空集合,如果存在一个法则f,使得对X中的每一个元素x,按法则f,在Y中有唯一确定的元素y与之对应,则称f为X到Y的映射,记作f∶X→Y其中y称为元素x(在映射f下)的象,记作f(x),即y=f(x)而元素x称为元素y(在映射f下)的一个原象,集合X称为映射f的定义域,记为Df;X中所有元素的象所组成的集合称为映射f的值域,记作Rf或f(X),即Rf=f(X)={
1.映射概念
定义1 设X,Y是两个非空集合,如果存在一个法则f,使得对X中的每一个元素x,按法则f,在Y中有唯一确定的元素y与之对应,则称f为X到Y的映射,记作
f∶X→Y
其中y称为元素x(在映射f下)的象,记作f(x),即
y=f(x)
而元素x称为元素y(在映射f下)的一个原象,集合X称为映射f的定义域,记为Df;X中所有元素的象所组成的集合称为映射f的值域,记作Rf或f(X),即
Rf=f(X)={f(x)x∈X}
2.满射
设f是从集合X到集合Y的映射,若
Rf=Y
即Y中的每一个元素y都是X中某元素的象,则称f为X到Y的满射.
3.单射
若对X的任意两个不同的元素x1,x2,即x1≠x2,它们的象也不同,即
f(x1)≠f(x2)(https://www.xing528.com)
则称f为X到Y的单射.
4.一一映射(单满射)
若映射f既是单射又是满射,则称f为一一映射,也称为单满射.
5.逆映射
如果f为X到Y的单满射,则对于每一个y∈Y,有唯一的x∈X,使f(x)=y,从而定义了一个从Y到X的映射g,即
g∶Y→X
这个映射g称为f的逆映射,记作f-1,其定义域Df-1=Y,值域Rf-1=X.
6.复合映射
设两个映射
g∶X→Y1,f∶Y2→Z
其中Y1⊆Y2,则由映射g和f可以定义一个从X到Z的对应法则,它将每一个x∈X映成
f[g(x)]∈Z
这个法则确定了一个从X到Z的映射,这个映射称为g和f构成的复合映射,记为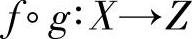 ,其中
,其中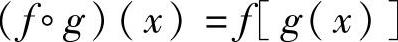 ,x∈X.
,x∈X.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




