热分析基础知识：了解ABAQUS有限元分析

热分析遵循热力学第一定律，即能量守恒定律。

对于一个封闭的系统（没有质量的流入或流出）：

Q-W=ΔU+ΔKE+ΔP E（15-1）

式中 Q—热量；

W—做功；

ΔU—系统内能；

ΔKE—系统动能；

ΔPE—系统势能。

对于大多数工程传热问题：ΔKE=ΔPE=0；

通常考虑没有做功：W=0，则：Q=ΔU；

对于稳态热分析：Q=ΔU=0，即流入系统的热量等于流出的热量；

对于瞬态热分析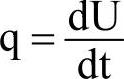：，即流入或流出的热传递速率等于系统内能的变化。

●热传导

热传导可以定义为完全接触的两个物体之间或一个物体的不同部分之间由于温度梯度而引起的内能的交换。热传导遵循傅立叶定律：

式中q"—热流密度（W/m²）；

k—导热系数（W/（m-℃））；

“-”—热量流向温度降低的方向。

●热对流

热对流是指固体的表面与它周围接触的流体之间，由于温差的存在引起的热量的交换。热对流可以分为两类：自然对流和强制对流。热对流用牛顿冷却方程来描述：

q′′=h（T_s−T_B）（15-3）

式中h—对流换热系数（或称为膜传热系数、给热系数、膜系数等）；

Ts—固体表面的温度；

T_B—周围流体的温度。

●热辐射

热辐射是指物体发射电磁能，并被其他物体吸收转变为热的热量交换过程。物体温度越高，单位时间辐射的热量越多。热传导和热对流都需要有传热介质，而热辐射无须任何介质。实质上，在真空中的热辐射效率最高。

在工程中通常考虑两个或两个以上物体之间的辐射，系统中每个物体同时辐射并吸收热量。它们之间的净热量传递可以用斯蒂芬—波尔兹曼方程来计算：

式中 q—热流率；(www.xing528.com)

ε—辐射率（黑度）；

σ—斯蒂芬-波尔兹曼常数，约为5.67×10−⁸W/m²·K⁴；

A₁—辐射面1的面积；

F₁₂—由辐射面1到辐射面2的形状系数；

T₁—辐射面1的绝对温度；

T₂—辐射面2的绝对温度。由上式可以看出，包含热辐射的热分析是高度非线性的。

●稳态传热

如果系统的净热流率为0，即流入系统的热量加上系统自身产生的热量等于流出系统的热量：q_流入+q生成-q流出=0，则系统处于热稳态。在稳态热分析中任一结点的温度不随时间变化。稳态热分析的能量平衡方程为（以矩阵形式表示）：

[K]{T}={Q}（15-5）

式中 [K]—传导矩阵，包含导热系数、对流系数及辐射率和形状系数；

[T]—结点温度向量；

[Q]—结点热流率向量，包含热生成。

ANSYS利用模型几何参数、材料热性能参数以及所施加的边界条件，生成[K]、[T]以及[Q]。

●瞬态传热

瞬态传热过程是指一个系统的加热或冷却过程。在这个过程中系统的温度、热流率、热边界条件以及系统内能随时间都有明显变化。根据能量守恒原理，瞬态热平衡可以表达为（以矩阵形式表示）：

式中 [K]—传导矩阵，包含导热系数、对流系数及辐射率和形状系数；

[C]—比热矩阵，考虑系统内能的增加；

{T}—结点温度向量；—温度对时间的导数；{Q}—结点热流率向量，包含热生成。

如果有下列情况产生，则为非线性热分析：

●材料热性能随温度变化，如K（T）、C（T）等；

●边界条件随温度变化，如h（T）等；

●含有非线性单元；

●考虑辐射传热。

非线性热分析的热平衡矩阵方程为：

式中各参数含义同式（15-6）。

ABAQUS热分析的边界条件或初始条件可分为7种：温度、热流率、热流密度、对流、辐射、绝热和生热。