【摘要】：瞬态动力学分析需要求解半离散的方程组。对于线性动力学问题，动力学行为由两个独立的特性决定：线弹性（动力）结构行为和施加的动力载荷。因此，求解动力学问题的一种方法是：首先可不考虑施加的载荷进行结构动力分析来确定特征值；其次基于结构的特征值和特征模态计算给定载荷历程的结构动力响应。另一种方法，动力学方程可以作为施加载荷的函数而直接积分。图12-5 瞬态动力学求解方法其中缩减矩阵和完整矩阵的主要区别如下。
瞬态动力学分析需要求解半离散的方程组。离散是指结构由离散的结点描述；半离散是指在方程的导出过程中，每个时刻都要满足平衡。在瞬态分析中，连续的时间周期分为许多时间间隔，并且只有在离散的时间上才能得到解。
对于线性动力学问题，动力学行为由两个独立的特性决定：线弹性（动力）结构行为和施加的动力载荷。
因此，求解动力学问题的一种方法是：首先可不考虑施加的载荷进行结构动力分析（即模态分析）来确定特征值；其次基于结构的特征值和特征模态计算给定载荷历程的结构动力响应。这一过程称为模态分析或模态叠加法。由于高阶模态不准确，因而比较成功的应用大都在于有低频范围的激振的结构。
另一种方法，动力学方程可以作为施加载荷的函数而直接积分。积分方法有多种，重要的一点就是稳定性和精度。这些方法可以用于短波长问题，只要有限元网格足够细密，就能够描述这些局部的现象。
这是瞬态分析的最一般形式，载荷可为时间的任意函数；对于线性问题矩阵[M]、[C]和[K]均与{u}及其时间导数无关。
基于求解方法，ABAQUS允许在瞬态动力分析中包括各种类型的非线性——大变形、接触问题及塑性材料等。常用的求解方法如图12-5所示。
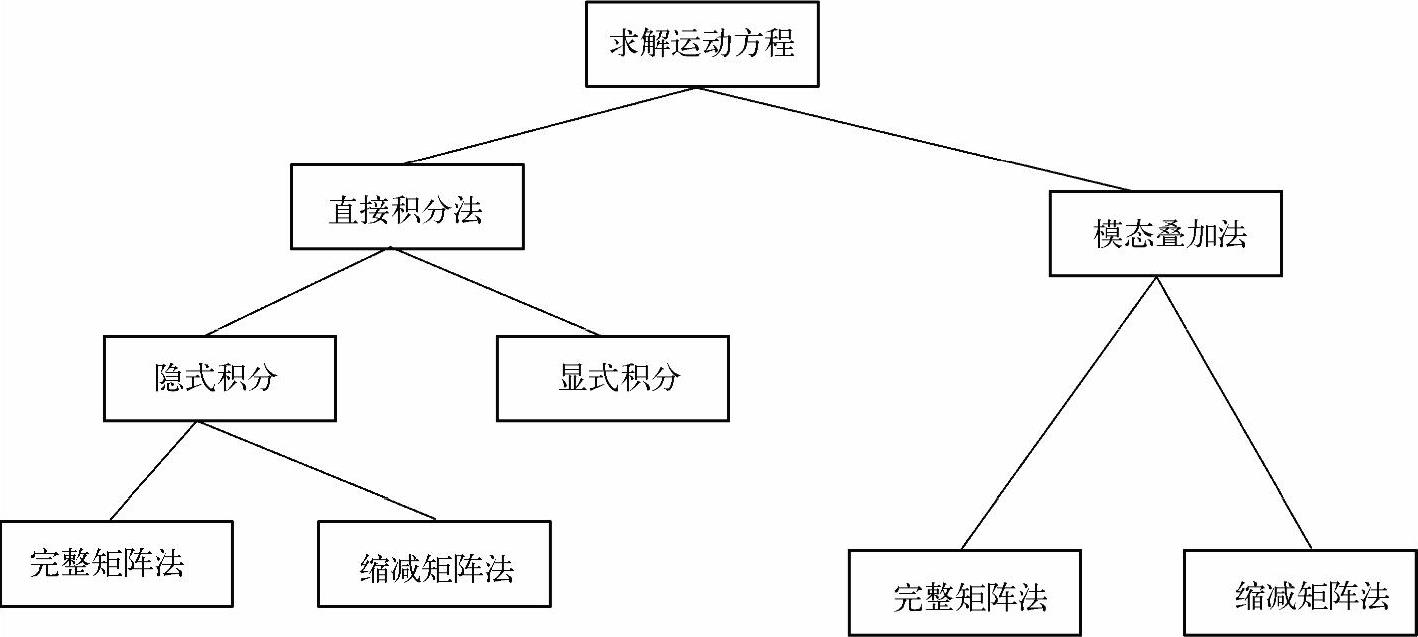
图12-5 瞬态动力学求解方法(www.xing528.com)
其中缩减矩阵和完整矩阵的主要区别如下。
（1）缩减矩阵：
■用于快速求解；
■根据主自由度写出[K]、[C]和[M]等矩阵，主自由度是完全自由度的子集；
■缩减的[K]是精确的，但缩减的[C]和[M]是近似的。此外，还有其他一些缺陷。
（2）完整矩阵：
■不进行缩减；
■采用完整的[K]、[C]和[M]矩阵。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
