阻尼与ABAQUS中的振型计算及设计分析

如果一个无阻尼结构作自由振动，则它的振幅会保持恒定不变。然而，在实际中由于结构运动而能量耗散，振幅将逐渐减小直至振动停止，这种能量耗散称为阻尼。通常假定阻尼为粘滞的或正比于速度。式（12-1）可以写成包含阻尼的形式：

式中 C——结构的阻尼阵；

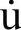——结构的速度。

能量耗散来自于诸多因素，其中包括结构结合处的摩擦和局部材料的迟滞效应。阻尼概念对于无需顾及能量吸收过程的细节表征而言是一个很方便的方法。

在ABAQUS中，是针对无阻尼系统计算其振型的。然而，大多数工程问题还是包含阻尼的，尽管阻尼可能很小。有阻尼的固有频率和无阻尼的固有频率的关系如式（12-10）所示：

式中 ω_d——阻尼特征值；

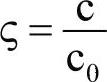——临界阻尼比；

c——该振型的阻尼；

c₀——临界阻尼。

对ς较小的情形（ς<0.1），有阻尼系统的特征频率非常接近于无阻尼系统的相应值。当ς增大时，采用无阻尼系统的特征频率就不太准确。当ς接近于1时，就不能采用无阻尼系统的特征频率了。

当结构处于临界阻尼（ς=1）时，施加一个扰动后，结构不会有摆动而是很快地恢复到静止的初始形态，如图12-2所示。

模拟动力学过程要定义阻尼。阻尼是分析步定义的一部分，每阶振型可以定义不同数量的阻尼。

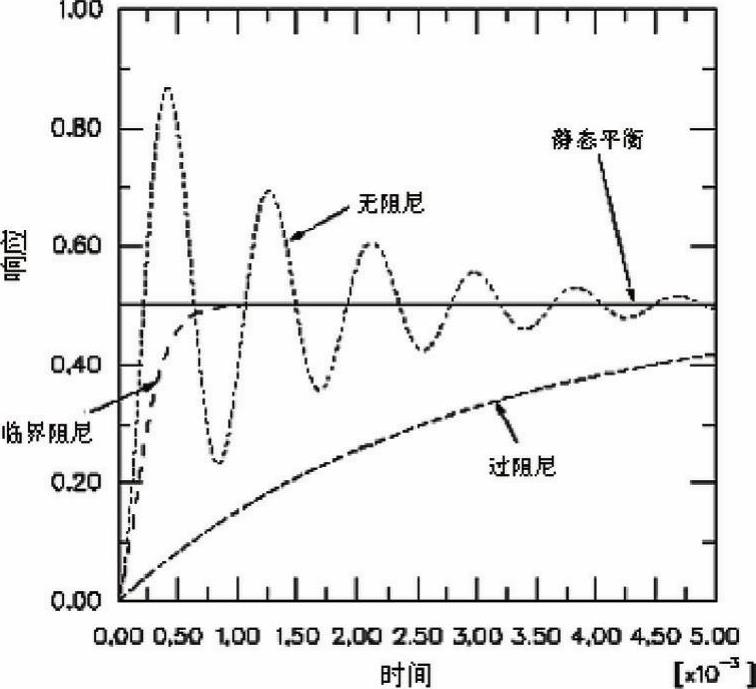
图12-2 临界阻尼状态

在ABAQUS中，为了进行瞬时模态分析，可定义不同类型的阻尼：直接模态阻尼，瑞利（Rayleigh）阻尼和复合模态阻尼。

■直接模态阻尼

采用直接模态阻尼可以定义对应于每阶振型的临界阻尼比ς。ς的典型取值范围是1%～10%。直接模态阻尼允许精确定义每阶振型的阻尼。(www.xing528.com)

■瑞利阻尼

瑞利阻尼假设阻尼矩阵是质量矩阵和刚度矩阵的线性组合：

C=αM+βK（12-11）

式中 α和β——用户定义的常数。

尽管假设阻尼正比于质量和刚度没有严格的物理基础，但实际上我们对于阻尼的分布知之甚少，也就不能保证使用更为复杂的阻尼模型是正确的。一般来讲，这个模型对于大阻尼系统——临界阻尼超过10%时，是失效的。相对于其他形式的阻尼，可以精确地定义系统每阶模态的瑞利阻尼。

■复合阻尼

在复合阻尼中，可以定义每种材料的临界阻尼比。复合阻尼是对应于整体结构的阻尼。当结构中有许多不同种类材料时，这一选项是十分有用的。

在大多数线性动力学问题中，恰当地定义阻尼对于获得精确的结果是十分重要的。但是阻尼只是对结构吸收能量这种特性的近似描述，而不是去仿真造成这种效果的物理机制。所以，确定分析中所需要的阻尼数据是很困难的。有时，可以从动力试验中获得这些数据，但是在多数情况下，需要通过经验或参考资料获得数据。在这些情况下，要仔细地分析计算结果，应该通过参数分析来评价阻尼系数对于模拟的敏感性。

事实上，ABAQUS的所有单元均可用于动力分析。选取单元的一般原则与静力分析相同。但是，在模拟冲击和爆炸载荷时，应选用一次单元。因为它们具有集中质量公式，在模拟应力波效果方面优于采用二次单元的一致质量公式。

在动力分析中，剖分网格需要考虑响应中将被激发的振型，网格剖分应能充分反映那些振型。因为能满足静态模拟要求的网格，不一定能计算高频振型的动态响应。

如图12-3所示的平板，用一次壳单元剖分的网格对于受均布载荷的静力分析以及一阶振型的预测是适用的。但是，该网格对于精确模拟第六阶振型就显得太粗糙了。

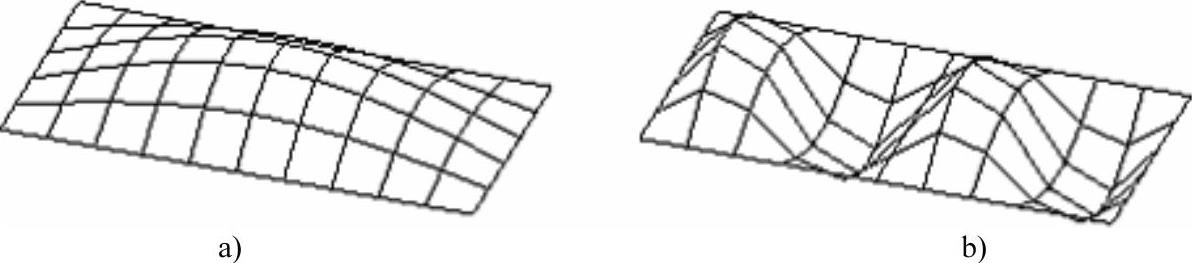
图12-3 平板的粗网格

a）模态1：31.1Hz b）模态6：140Hz

图12-4显示了同样的板用一次单元进行更精细的网格剖分后所模拟的结果。由图中可看出，第六阶振型的位移看起来明显较好，预测的频率也更为准确。因此，可以得出：如果作用在板上的动载会显著地激发该阶振型，则应采用精细的网格；采用粗网格将得不到精确的结果。

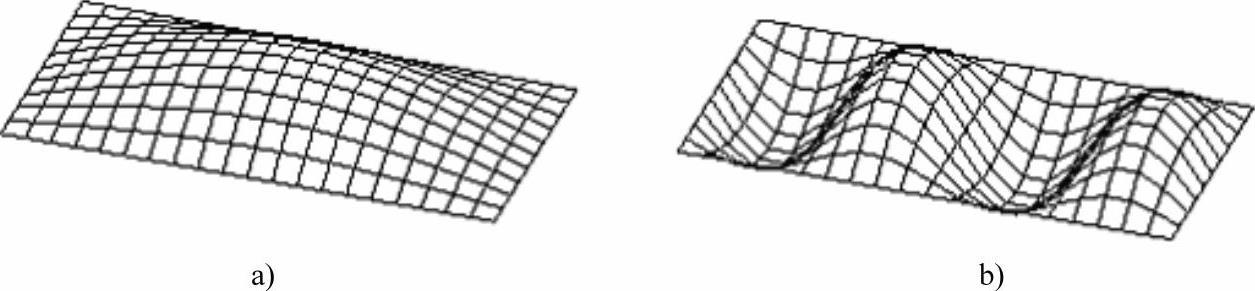
图12-4 平板的精细网格

a）模态1：30.2Hz b）模态6：124Hz