ABAQUS梁单元特性与使用

对于某一方向尺寸（长度方向）明显大于其他两个方向的尺寸，并且以纵向应力为主的结构，ABAQUS用梁单元对它模拟。梁的理论基于这样的假设：结构的变形可以全部由沿梁长度方向的位置函数来决定。当梁的横截面的尺寸小于结构典型轴向尺寸的1/10时，梁理论能够产生较精确的结果。常见的典型轴向尺寸如下：

●支承点之间的距离；

●有重大变化的横截面之间的距离；

●所关注的最高振型的波长。

ABAQUS梁单元假定梁横截面与梁的轴向垂直，并在变形时保持平面。

要注意并不是所有梁单元的横截面的尺寸必须小于典型单元长度的1/10，因为高度精细的网格可能包含长度小于横截面尺寸的梁单元，不过并不推荐这种方式，这种情况下更适合使用实体单元。

在ABAQUS中梁单元的名字以字母“B”开头。下一个字符表示单元的维数：“2”表示二维梁单元，“3”表示三维梁单元。第三个字符表示插值的阶数：“1”表示线性插值，“2”表示二次插值，“3”表示三次插值。

■梁单元库 梁单元库中有二维和三维的线性、二次及三次梁单元。

■自由度

三维梁单元每个结点有6个自由度：3个平动自由度（1～3）和3个转动自由度（4～6）。“开口截面”型的梁（例如B31OS）有一个表示梁横截面翘曲量的附加自由度（7）。

二维梁单元的每个结点有3个自由度：2个平动自由度（1和2）和1个绕模型所在平面法线的转动自由度（6）。

■单元性质

所有的梁单元必须有梁截面特性，它规定了梁的材料性质和梁横截面轮廓线。结点坐标只定义了梁的长度，用户必须给出梁截面轮廓线的几何尺寸和形状。换言之，用户可以通过给定截面面积和惯性矩这类工程特性参数来定义一个一般的梁截面轮廓线。

若用户定义了梁截面的几何轮廓线，ABAQUS就会用数值积分方法计算横截面性质，材料可以是线性或非线性的。

若用户用截面的面积，惯性矩和扭矩等工程特性参数来代替指定横截面尺寸，则ABAQUS就不必对横截面积分，这种情况计算量较小。在用这个方法时，材料可以是线性或非线性的。此时，根据力和弯矩结果来计算响应，只有在特别请求时才计算应力和应变。

●梁横截面的几何形状

如果用梁横截面的形状和尺寸来定义梁的外形，ABAQUS提供了如图7-38所示的各种常用的梁横截面形状以便选用。其中的任意多边形横截面可以定义任意形状的薄壁截面梁。详情可参考ABAQUS用户手册的相关章节。

图7-38 梁横截面形状

a）任意多边形梁 b）箱式梁 c）圆梁 d）六边形梁 e）工字梁 f）L形梁 g）管形梁 h）矩形梁 i）梯形梁

在定义梁横截面的几何形状时，ABAQUS/CAE会提示输入所需尺寸，不同的横截面类型会有不同的尺寸要求。

如果梁的外形与梁横截面的截面性质有关时，可以要求在分析过程中计算横截面的工程特性参数，也可以要求在分析开始前预先计算横截面的工程特性参数。当材料的力学特性既有线性又有非线性时（例如，截面刚度因塑性屈服而改变），可以选用第一种方式；而对线弹性材料，第二种方式效率更高。

此外，也可以不给出横截面尺寸，而直接给出横截面的工程特性参数（面积、惯性矩和扭转常数），这时材料的力学特性既可以是线性的也可以是非线性的。这样就可以组合梁的几何和材料特性来定义梁对载荷的响应，同样，响应也可以是线性或非线性的。详情可参考ABAQUS用户手册中相关章节。

●截面计算点

梁横截面的几何形状和尺寸确定后，就要在分析过程中计算横截面的工程特性参数，ABAQUS用一组分布于梁横截面上的计算点来计算梁单元的响应。横截面计算点的编号以及位置详见ABAQUS用户手册相关章节。单元的变量如应力和应变等，可在任意一个横截面计算点上输出。然而，默认的输出点只在几个指定的横截面计算点上给出，详见ABAQUS用户手册相关章节。

图7-39所示，为一矩形梁单元内的积分点和默认横截面点示意图。对该横截面，只有计算点1、5、21和25的值是默认输出，图7-39所示的梁单元总共使用50个横截面计算点（每两个结点之间25个）来计算单元刚度。若选择预先计算横截面特性参数，ABAQUS不在截面计算点上计算梁的响应，而是根据梁截面的工程特性参数确定截面的响应。因而，此时ABAQUS只把截面计算点作为输出结果的位置，所以要指定需输出结果的截面计算点。

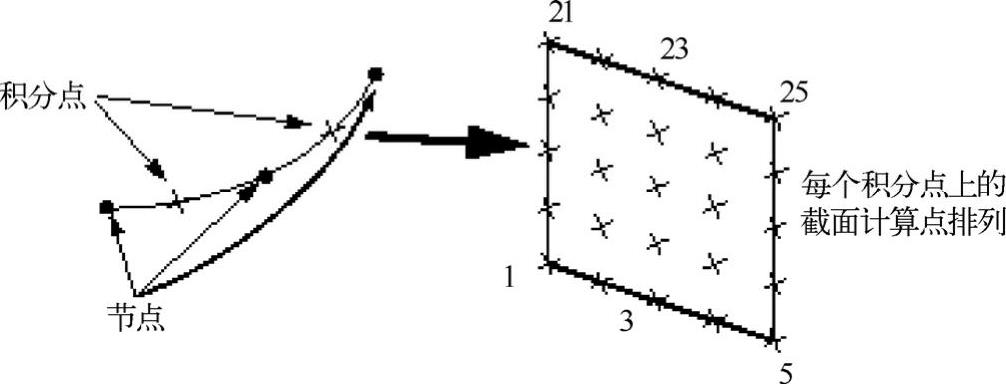
图7-39 B32矩形梁单元内的积分点和默认横截面点

●横截面定向

用户必须在全局直角坐标空间（GCS）中定义梁横截面的方向。从单元的第一结点到下一个结点的矢量被定义为沿着梁单元的局部切线t，梁横截面与局部切线矢量t垂直。由n₁和n₂代表局部梁横截面轴（1-2）。这三个矢量t、n₁、n₂构成了右手法则的局部直角坐标系，如图7-40所示。

图7-40 梁单元切向矢量t，梁横截面轴n₁和n₂的取向

对于二维梁单元，n₁的方向总是（0.0，0.0，-1.0）。

对于三维梁单元可用几种方法来定义局部梁横截面轴的方向。

第一种方法是在数据行中指定一个附加的结点来确定单元方位（这种方法要用手动编辑ABAQUS/CAE产生的输入文件）。从梁单元的第一结点到附加结点的矢量V（见图7-40），初步作为n₁的近似方向。然后，ABAQUS把t×V作为梁的n₂方向，在n₂确定后，ABAQUS再定义真正的n₁方向为n₂×t，上述过程确保了局部切线矢量和局部梁横截面轴构成正交系。

第二种方法是在ABAQUS/CAE中定义梁截面特性时，给定一个近似的n₁方向，然后ABAQUS会按上述过程计算实际的梁截面轴。如果在指定一个附加结点的同时又给出一个近似的n₁方向，ABAQUS将优先采用前者。

如果没有提供近似的n₁方向，ABAQUS将把从原点到点（0.0，0.0，-1.0）的矢量作为默认的n₂方向，这可算作第三种方法。

有两种办法可以用来覆盖被ABAQUS定义的n₂方向，两种办法都要求手动编辑输入文件。一种是把n₂矢量的分量作为第4、5、6个数据值紧跟在结点坐标数据后面给出；另一种是使用*NORMAL选项直接指定法线方向（该选项可以使用ABAQUS/CAE中的Keywords Editor添加上）。如果两种办法都使用，则后者优先。ABAQUS再定义方向n₁为n₂×t。

用户给出的n₂方向不必与梁单元切线t垂直，当n₂方向确定后，局部梁单元切线可以重新定义为n₁×n₂的值。这样再定义的局部梁切线t，很可能与从第一结点到第二结点的矢量所定义的梁轴线不一致。如果n₂方向对垂直于单元轴线平面的转角超过了20°，ABAQUS将在数据文件中给出一个警告信息。

●梁单元曲率

梁单元的曲率是基于梁的n₂方向相对于梁轴的方向来确定的。如果n₂方向不与梁轴的正交（即梁轴向和切向量t不一致），则认为梁单元有初始弯曲。由于曲梁和直梁的性能不同，用户必须检查模型以确保应用正确的法线和曲率。对于梁和壳体，ABAQUS使用同样的算法来确定几个单元公共结点的法线。请参阅ABAQUS用户手册相关章节。

如果用户打算模拟曲梁结构，可能应当使用前面所介绍的直接定义n₂方向的两种方法之一，它允许用户有很大的控制权来模拟曲率。即使用户打算模拟直梁，也可以引入曲率作为公共结点的平均法线。

●梁横截面的结点偏移

当梁单元作为壳模型的加强部件时，如果梁单元和壳单元有共同结点分析过程就很方便。壳单元结点位于壳的中面上，梁单元结点位于梁横截面的某处。因此，如果要壳和梁单元有共同结点，壳和加强梁就会重叠，除非梁横截面从结点位置处偏移，如图7-41所示。

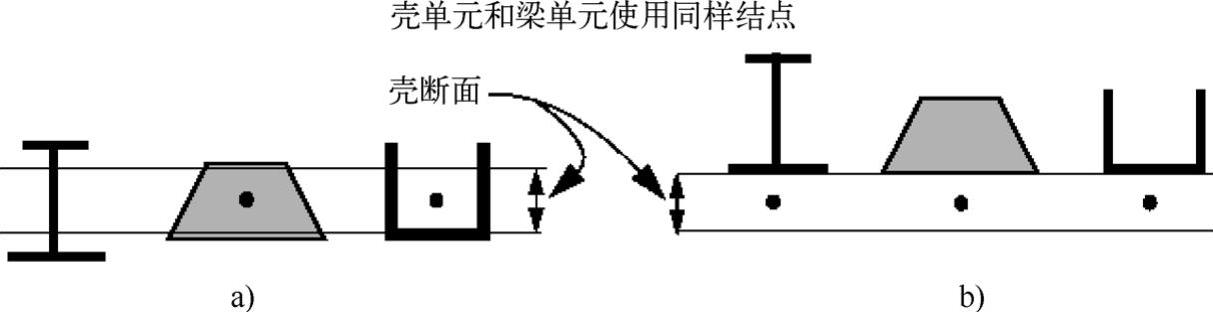
图7-41 梁单元作为壳单元的加强部件

a）梁截面无偏移 b）梁截面有偏移

对于工字型、梯型和任意多边形的梁横截面，可以定义该截面形状位于离截面局部坐标系原点某一距离，且使它等于偏离单元结点的距离。由于很容易使这几种形状梁的横截面偏离梁的结点，它们可以作为图7-41b所示的加强部件（如果加强部件的凸缘或网翼翘曲很重要，则应该用壳单元来模拟）。

图7-42所示的工字型梁附着在一个1.2个单位厚的壳上。可以给位于梁截面底部的结点定义一个偏移量来确定梁截面的位置，此处的偏移量为0.6，即壳厚度的一半。

图7-42 工字型梁用作壳单元的加强部件

同样也可以指定形心和剪切中心的位置，它们的位置可以由梁的结点偏移值来确定，这样也可以形成刚度。

另外也可以分别定义梁单元和壳单元，然后用两个结点间的刚梁约束来连接它们。详细情况可参阅ABAQUS用户手册的相关章节。

■单元列式和积分

ABAQUS中的所有梁单元都是梁柱类单元—这意味着单元可以有轴向、弯曲和扭转变形。此外，Timoshenko梁单元还要考虑横向剪切变形的影响。(www.xing528.com)

●剪切变形

线性单元（B21和B31）及二次单元（B22和B32）是考虑剪切变形的Timoshenko梁，因此，它们适合于模拟剪切变形起重要作用的深梁和剪切变形不太重要的细长梁。这些单元横截面的特性与厚壳单元相类似，如图7-43b所示。

图7-43 剪切梁的截面特性

a）Euler-Bernoulli梁 b）Timoshenko梁

ABAQUS假设这些梁单元的横向剪切刚度为线弹性常量。另外，构造这些梁的列式使它们的横截面积可以作为轴向变形的函数而改变，在几何非线性场合还要考虑非零泊松比的影响。

只要梁的横截面尺寸小于结构典型轴向尺寸的1/10，使用这些单元就可以得出有用的结果。通常认为这是梁理论适用性的界限。此外，如果梁横截面在弯曲变形时不能保持平面，梁单元就不适合模拟这种变形。

三次单元被称为Euler-Bernoulli梁单元（B23和B33），它们不能模拟剪切柔度。这些单元的横截面保持与梁轴线垂直，如图7-43a所示。

因此，用三次单元模拟相对细长的构件更为有效。由于三次单元的位移变量沿单元长度方向为三次方，故在静态分析中，常用三次单元模拟结构构件，但在动态分析中要尽量少用这种单元。三次单元总是假设单元的剪切变形可以忽略。

一般情况下，只要横截面的尺寸小于典型轴向尺寸的1/15，这个假设就是有效的。

●扭转响应-翘曲

结构构件经常承受扭矩，几乎所有的三维框架结构都会发生这种情况。在一个构件中引起弯曲的载荷在另一个构件中可能引起扭转，如图7-44所示。

梁对扭转的响应依赖于它的横截面形状。一般说来，梁的扭转会使横截面产生翘曲或非均匀的离面位移。ABAQUS只考虑三维梁单元的扭转和翘曲的影响。翘曲计算假设翘曲位移是小量。

以下各种梁截面在受扭时的力学行为是不同的。

图7-44 框架结构中的扭转

■实心横截面

在扭转作用下，非圆形的实心横截面不再保持平面而是发生翘曲。ABAQUS应用St.Venant翘曲理论计算由翘曲引起的每一横截面点处的剪切应变分量。

这种横截面的翘曲被认为是自由的，翘曲产生的轴向应力可以忽略不计（翘曲约束仅仅影响非常靠近约束端处的结果）。

实心横截面梁的扭转刚度取决于材料的剪切模量G和梁横截面的扭转常数J。J取决于梁的横截面形状和翘曲特征。对于在横截面上产生较大非弹性变形的扭转载荷，用这种方法模拟是不够精确的。

■闭口薄壁横截面

闭口薄壁非圆形横截面的梁（箱式或六边形）具有明显的抗扭刚度，因此，其性质与实心横截面类似。ABAQUS假设横截面翘曲也是自由的。

基于横截面的薄壁性质，ABAQUS假设剪应变沿壁厚是个常数。当壁厚是典型横截面尺寸的1/10时，薄壁假设是有效的。常见的薄壁横截面的典型横截面尺寸包括：

（1）圆管横截面的直径；

（2）箱式横截面的边长；

（3）任意形状横截面的典型边长。

■开口薄壁横截面

开口薄壁横截面在扭矩作用下发生无约束翘曲时的刚度非常小，而这种结构的抗扭刚度的主要来源是对轴向翘曲应变的约束。对开口薄壁梁翘曲的约束导致了轴向应力，而该应力却会影响梁对其他载荷类型的响应。

ABAQUS有剪切变形梁单元B31OS和B32OS，它们包含了对开口薄壁横截面的翘曲影响。当承受明显的扭转载荷时，必须使用这些单元来模拟具有开口薄壁横截面的结构，例如管道（定义为任意多边形横截面）或者工字型横截面。

●翘曲函数

翘曲导致的沿梁横截面变化的轴向变形可用翘曲函数来描述。在开口横截面单元中，用一个附加的自由度7来描述这个函数的量值。

约束这个自由度可以使其在施加约束的结点处不发生翘曲。因为在每个构件上的翘曲幅度不同，所以在开口横截面梁框架结构的连接点处，一般每个构件使用各自的结点，如图7-45所示。

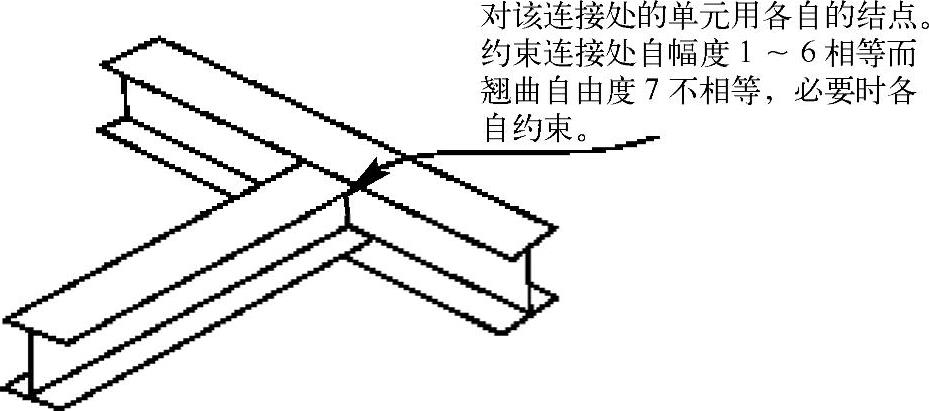
图7-45 开口薄壁梁的连接

然而如果连接方式设计为防止翘曲的，那么所有构件应使用一个公共的结点，而且必须约束翘曲自由度。

当剪力不通过梁的剪切中心时会产生扭转，扭转力矩等于剪力乘以它到剪切中心的偏心距。对于开口薄壁梁，形心和剪切中心常常不重合，如图7-46所示。

图7-46 一些梁横截面的剪切中心s和形心c的近似位置

如果结点不是位于横截面的剪切中心，那么在载荷作用下横截面可能会发生扭曲。

ABAQUS中，线性梁单元（B21和B31）和二次梁单元（B22和B32）允许剪切变形，并考虑了有限轴向应变；它们不仅适合于模拟细长梁，也适合于模拟短梁。

尽管三次梁单元（B23和B33）允许梁有大位移和大转动，但不考虑剪切柔度，并且假定轴向应变很小，因此，它们适合于模拟细长梁。

ABAQUS提供线性和二次梁单元的变种单元（B31OS和B32OS）来模拟薄壁开口梁。这些单元能正确地模拟开口横截面的扭转和翘曲效应，例如I-型和U-型槽钢。

ABAQUS也提供杂交梁单元来模拟非常细长的构件，例如海上石油平台上的柔性立管和模拟非常刚硬的连接件。

■单元输出变量

三维剪切变形梁单元可输出应力分量：轴向应力（σ11）和扭转引起的剪应力（σ12）。在薄壁截面梁中剪应力沿截面的壁作用，相应的应变量也可以输出。剪切变形梁单元也可输出截面上的横向剪力。

细长（三次）梁的输出结果只有轴向变量。空间开口截面梁的输出结果也只有轴向变量，因为此时的扭转剪应力可略去。

所有的二维梁单元只输出轴向的应力和应变。

根据用户需要，轴向力、弯矩和绕局部梁轴的曲率也可以输出。至于哪种单元提供哪些分量的详细情况，可以查阅ABAQUS用户手册的相关章节。

■梁单元的选择

●对任何涉及接触的分析，应使用一阶的、有剪切变形的梁单元（B21，B31）。

●对于结构刚度非常大或者非常柔软的结构，在几何非线性分析中应当使用杂交梁单元（B21H，B32H等）。

●Euler-Bernoulli三次梁单元（B23，B33）在模拟承受分布载荷作用的梁，包括动态的振动分析时，会有很高的精度。如果横向剪切变形也很重要，则使用Timoshenko二次梁单元（B22，B32）。

●模拟有开口薄壁横截面的结构应当使用开口横截面翘曲理论的梁单元（B31OS，B32OS）。