B样条有一种直观而有趣的解释,即B样条的几何解释:多元光滑分片多项式可以看作高维空间多面体的“切片”体积.由于计算多面体体积问题的复杂性,在历史上人们并没有沿着这个方向来研究多元样条函数,而是通过广义函数的定义方式发展了多元样条函数理论.伴随样条函数理论的发展成熟,产生了很多计算工具,而与多面体体积计算相关联的领域,比如超平面配置领域的研究,仍然沿用代数几何或者李代数的方法,发展了众多计多面体体积的公式和定理.这些定理和公式在很大程度上与样条理论等价,而且两个分支在互不知晓的情况下各自独立地发展了30多年.很自然地,人们会想到可否利用多元样条的理论来研究多面体体积问题.这样便能建立多元样条函数与多个数学分支的紧密关联,从而体现数学的相关性与和谐性.这方面的研究起始于贾荣庆[77]关于幻方猜想的证明,此后,我国数学家许志强研究员系统地研究了这一关联,做出了很多原创性的贡献.本节主要介绍多面体体积与多元样条函数的联系,梳理前人的工作,并且提出未来的发展方向.本章的最后附上I.J.Schoenberg与H.B.Curry的通信,再现B样条理论的历史发展脉络.
Curry和Schoenberg在文献[24]中给出了一元B样条的几何解释,即



因此,Curry-Schoenberg给出了一元B样条的一种几何解释[24]
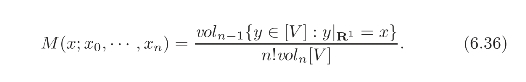
这个公式表明,B样条可以看作是单纯形的“切片”体积(见图6.1).
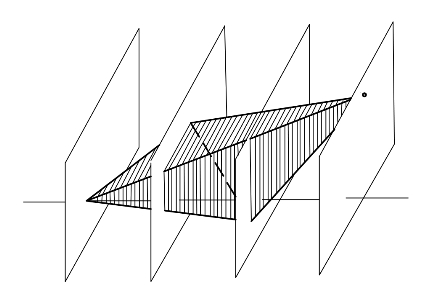
图6.1 由单纯形切片面积得到的一元二次B样条
特别地,当公式(6.36)中的n=1时,该公式退化为区间[x0,xn]的特征函数.当然,我们也要指出公式(6.36)对于任何满足条件vi|R=xi,i=0,1,···,n和voln[V]>0的向量v0,···,vn都成立.公式(6.36)表明M(x;x0,···,xn)恰好是超平面{y∈[V]:y|R1=t}和单纯形[V]的截面面积与该单纯形自身体积的比值.若取[V]为单位立方体[0,1]n,则得到Box样条;若取[V]为单纯形,则得到单纯形样条;若取[V]为[0,+∞),则得到截断幂函数.这些解释,使得B样条函数在其他数学分支,如代数几何、组合数学、离散数学等,有着诸多重要的应用.在此,我们仅给出公式(6.36)在研究B样条性质方面的两个应用结果.
首先,利用公式(6.36)给出一元B样条的下界.
定理6.3

特别地,在区间(x0,xn)上,M(x;x0,···,xn)恒正.(https://www.xing528.com)


下面的证明要用到Brunn-Minkowski不等式(Milman和Schecktman在文献[78]中给出了这个不等式的证明),即:对于任何Rn-1中的两个非空凸集A1,A2,有如下的不等式成立
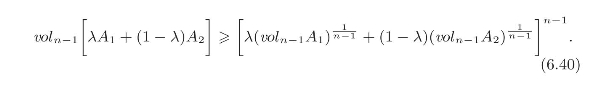
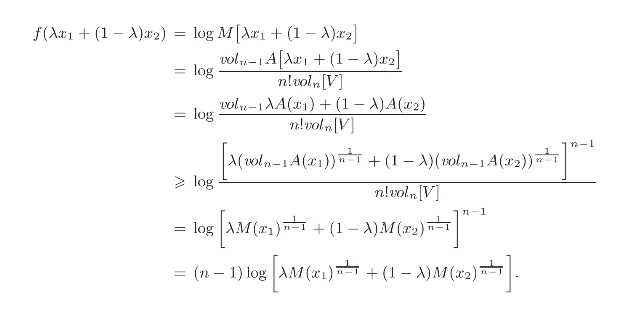
由于对数函数在(0,+∞)上是凹函数,即g(x)=log x,则对于任意的λ∈[0,1],x1,x2∈(0,+∞),有g(λx1+(1-λ)x2)≥λg(x1)+(1-λ)g(x2).
因此,可以得到
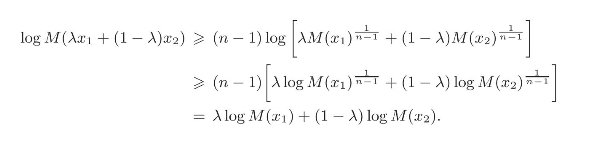
从而证明了一元B样条M(x;x0,···,xn)在其定义域内具有对数凹性质.
在Charles A.Micchelli的Mathematical Aspects of Geometric Modeling(1995)一书中,对公式(6.36)的评价“我们没有意识到关于公式(6.36)的任何应用,然而在Schoenberg的脑海里应该有着对这一解释的清楚认识”.在Schoenberg 1965年写给布朗大学的P.Davis信中,Schoenberg描述了一种构造二元B样条的方法.我们在本章的末尾会附上这封信的原文,以及历史上其他关于构造多元样条的记录.Schoenberg在信中画了一个关于二元二次样条的草图,这个草图能够清楚地显示出二元样条曲面在顶点附近的截面由一元B样条所构成.
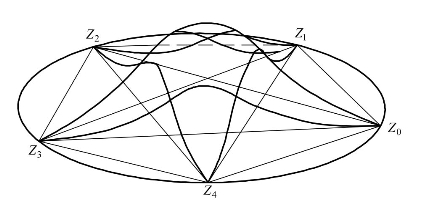
图6.2 一元二次B样条
然而,Micchelli对公式(6.36)的评价还为之过早.我国青年数学家许志强[79]在其博士论文中最先给出了公式(6.36)的在组合数学和离散几何学中的应用.由于计算多面体体积的复杂性,人们利用多面体体积研究样条函数的性质成为不大可能实现的奢望.这就是Micchelli等学者没有对这一样条几何解释进行深入研究的原因.但是,随着多元样条函数理论的发展,尤其是随着Box样条、单纯形样条、多元截断幂函数的理论研究的成熟,人们利用样条函数来研究与多面体体积相关联的问题成为可能.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




