【摘要】：众所周知，m次Hermite多项式Hm（x），可以由Gauss函数G（x）=的导函数所定义从而Hermite多项式的直交性质可以看作是Gauss函数的导函数与Hermite多项式之间的一种双正交关系.本章主要给出了渐近于Hermite多项式和Laguerre多项式的函数列的判定定理（定理5.3、定理5.5、定理5.6）.首先从Hermite多项式与Gauss函数的关系入手，研究了渐近于Gauss函
众所周知，m次Hermite多项式Hm（x），可以由Gauss函数G（x）=
的导函数所定义
从而Hermite多项式的直交性质
可以看作是Gauss函数的导函数与Hermite多项式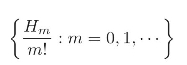
之间的一种双正交关系.(www.xing528.com)
本章主要给出了渐近于Hermite多项式和Laguerre多项式的函数列的判定定理（定理5.3、定理5.5、定理5.6）.首先从Hermite多项式与Gauss函数的关系入手，研究了渐近于Gauss函数的函数类φ，从而给出渐近于Hermite直交多项式的一类Appell多项式的构造方法，使得该序列与φ的n阶导数之间构成了一组双正交系统.利用这一结果，可以得到多种直交多项式和组合多项式的渐近性质以及一些新的组合恒等式.特别地，由N阶B样条所生成的Appell多项式序列恰为N阶Bernoulli多项式.Bernoulli多项式与B样条的导函数之间便构成了一组双正交系统，且标准化之后的Bernoulli多项式随着N→∞渐近到Hermite多项式.Euler多项式是由二项分布所生成的具有双正交性质的Appell序列，从而以Hermite直交多项式为渐近函数.同时给出了收敛到Laguerre多项式的函数列的构造方法.利用这些方法，验证了部分Askey格式成立.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
