Eulerian数、混合体积与B样条的细化

定义4.1　对于λ，μ≥0，凸多面体P1和P1定义Minkowski和

根据这一定义，Minkowski[50]提出了更为重要的混合体积的概念（尽管他只研究了d≤3的情形）.

证明　由B样条的几何解释，我们有

由公式（4.13）可知

类似地，该定理表明了单位立方体相邻切片Tk和Tk+1的混合体积与B样条的关系.

推论4.1　当λ≥0时，

基于上述推论，可以得到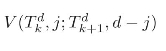的显式表达式.

推论4.2

推论4.1给出了特殊情况下混合体积的样条解释.混合体积在组合序列的对数凹性研究中具有十分重要的地位.美国科学院院士Richard P.Stanley[11]和教授Francesco Brenti[12][13]等人在这一领域的综述性文献中多次提到研究组合数的对数凹性质的混合体积方法.Schmidt和Simion[14]于1997年也曾提出与混合体积相关的公开问题4.1.混合体积计算的复杂性，使得这一方向的研究仍然处于初级阶段.多元样条在多面体体积计算方面具有独特的优势，而混合体积可以看作是一般体积的推广.因此，我们希望借助样条函数来研究一般意义下的混合体积计算.我们提出如下问题：

问题4.2　混合体积V（P1，d-j；P2，j）如何用样条函数表示？(www.xing528.com)

如果能够得到混合体积的样条表示，则可以利用多元样条函数在递归计算方面进行系统的研究[21]，为混合体积的计算提供快速算法.更进一步，可以定义出一类具有对数凹性质的组合序列.从而可以部分回答Schmidt和Simion[14]提出的公开问题.

目前我们可以给出一些特殊情况下混合体积的样条解释.有如下定理成立.

定理4.3　若两个凸多面体定义为

且它们的混合体积为

我们有

其中，b1，b2为整数且有b2=mb1+q.

证明　由B样条的几何解释可知

不妨令μ=1，则由式（4.16）得